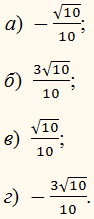Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
ВЫРАЖЕНИЕ ВСЕХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ОДНУ ИЗ НИХ
или посмотрите
ВИДЕО УРОК
1. Дано: соs α = 0,8.
Найдите tg α, если 3π/2
< α
< 2π.
а) 0,25;
б) 0,75;
в) –0,75;
г) –0,25.
2.
Дано: sin α = 40/41.
Найдите соs α, если π/2 < α < π.
а) –9/41;
б) 9/43;
в) 9/41;
г) –9/43.
3. Дано: sin α = 40/41.
Найдите tg α, если π/2 < α < π.
а) –44/7;
б) 44/9;
в) 44/7;
г) –44/9.
4. Дано: sin α = 40/41.
Найдите сtg α, если π/2 < α < π.
а) 9/41;
б) –9/40;
в) –9/41;
г) 9/40.
5. Дано: соs α = 4/5.
Найдите sin α, если 3π/2
< α
< 2π.
а) –3/5;
б) –3/7;
в) 3/7;
г) 3/5.
6. Дано:
соs α = 4/5.
Найдите tg α, если 3π/2 < α < 2π.
а) –3/5;
б) 3/4;
в) –3/4;
г) 3/5.
7. Дано:
соs α = 4/5.
Найдите сtg α, если 3π/2 < α < 2π.
а) –11/5;
б) –11/3;
в) 11/3;
г) 11/5.
8. Дано: tg α = 1.
Найдите соs α, если π < α < 3π/2.
Найдите сtg α, если π < α < 3π/2.
а) 1;
б) –3;
в) –1;
г) 3.
11. Дано: сtg α = 3.
Найдите соs α, если 0 < α < π/2.
