ВИДЕО УРОК
Инертность, которой обладает каждое тело, – одно из важнейших его свойств,
потому что от неё зависит ускорение тела в результате его взаимодействия с
другими телами.
Всякое свойство тел выражается определённой величиной.
Свойство тел занимать часть пространства выражается его объёмом.
Свойство тел, которое названо инертностью, тоже выражается особой
величиной. Такой величиной является масса.
То из двух взаимодействующих
тел, которое получает меньшее ускорение, то есть более инертно, имеет большую
массу. Если обозначить массы взаимодействующих тел через m1 и m2, то можно предположить,
чтоОтношение абсолютных значений ускорений двух взаимодействующих тел равно обратному отношению их масс.
ПРИМЕР:
Отношение ускорения алюминиевого цилиндра к ускорению стального равно трём. Это вызвано тем, что масса алюминиевого цилиндра в три раза меньше массы стального цилиндра.
Чтобы найти отношение масс двух тел нужно измерить их ускорения при взаимодействии.
Для определения массы отдельного тела надо поступить также как и при
измерении других величин. Для определения числа, выражающего длину тела надо
сравнить её с эталоном длины – метром.
Таким же способом определяют
численные значения масс; чтобы найти число, выражающее массу отдельного тела,
нужно сначала выбрать какое-нибудь тело, массу которого условно принимают за
единицу, – эталон массы. Затем провести опыт. В этом опыте тело, масса которого
определяется (измеряется), должно как-то взаимодействовать с эталоном массы. Схема
такого опыта показана на рисунке.Тогда оба они, и тело, и эталон, получат ускорения, которые можно измерить, и тогда можно написать равенство
или
где
– масса и ускорение тела, а
– масса и ускорение эталона. Но масса эталона равна единице, поэтому
Масса тела – это величина, выражающая его инертность. Она определяет отношение ускорения эталона массы к ускорению тела при их взаимодействии.
На Международном конгрессе в 1889 г. в качестве эталона массы была принята масса специально изготовленного цилиндра из сплава платины и иридия. Масса этого цилиндра и есть международная единица массы – килограмм (сокращённо: кг). Эталон массы хранится в Международном бюро мер и весов (Франция). В некоторых других странах имеются копии этого эталона. С достаточной точностью можно считать, что массой в 1 кг обладает 1 л чистой воды при 15°С.
Масса наряду с такими величинами, как длина и время, входит в число
основных величин систем единиц СИ и СГС. В системе СГС за единицу массы
принимается грамм (сокращённо: г):
1 г = 0,01 кг.
Одним из способов измерения массы – взвешивание, которым обычно и пользуются.
Но в некоторых случаях определение массы по ускорениям при взаимодействии является единственно возможным способом. Нельзя, например, взвешиванием измерить массу планет, звёзд и других небесных тел. На весах нельзя также измерять очень малые массы, например массы атомов и частиц, из которых они состоят.
Масса тела выражает его собственное свойство (инертность), которое не
зависит ни от того, в каких взаимодействиях тело участвует, ни от того, как оно
движется. Что бы с телом ни происходило, где бы оно ни находилось, как бы оно
ни двигалось, масса его остаётся одной и той же.
Об одном интересном и важном свойстве массы можно узнать, если поставить
следующий опыт.
ОПЫТ:
Соединим вместе два одинаковых алюминиевых цилиндра и поместим в центробежную машину.
Теперь стальной цилиндр взаимодействует не с одним, а с двумя соединёнными вместе алюминиевыми цилиндрами. Опыт показывает, что отношение ускорения соединённых вместе двух алюминиевых цилиндров к ускорению стального цилиндра равно не 3, а 3/2. Это значит, что масса двух одинаковых цилиндров, соединённых вместе и ставших как бы одним телом, вдвое больше массы одного из них.
Следовательно, когда два или несколько тел соединяются в
одно, их массы складываются.
Из-за этого свойства массы иногда говорят, что масса выражает собой и
количество вещества в теле. Ясно ведь, что в двух алюминиевых цилиндрах вдвое
больше алюминия, чем в одном.
Основные свойства массы.
– масса – скалярная величина, следовательно, инертные свойства тел одинаковы во всех направлениях.
– масса не зависит от характера движения точки.
– масса не зависит от физических условий, в которых
находится тело (от температуры окружающей среды, от наличия электромагнитных
или гравитационных полей).
– масса – величина аддитивная, то есть масса составного
тела равна сумме масс его частей.
Закон сохранения массы.
Масса замкнутой системы остаётся неизменной при любых механических процессах, происходящих в этой системе.
Масса Земли.
Массу Земли нельзя измерить, положив её на весы. Но её можно вычислить, пользуясь формулой для ускорения свободного падения:
Отсюда для величины массы Земли получаем:
Численные значения
были в своё время определены опытным путём:
и
Средний радиус Земли тоже хорошо известен:
R = 6370 км = 6,37 × 106 м.
Подставляя численные значения
в формулу для М, получаем:
Масса Земли равна почти шести миллионам миллиардов миллиардов килограмм !
Масса Луны.
В качестве примера того, как определяют массу тел по их ускорениям при взаимодействии, найдём массу Луны по её взаимодействию с Землёй.
О том, что Земля влияет на движение Луны, известно всем. Именно под
влиянием Земли Луна движется вокруг Земли по окружности радиусом около 384 000 км.
Обычно считают, что Луна обращается вокруг Земли так, как будто центр Земли
есть неподвижный центр лунной орбиты. Но этого не может быть, потому что при
взаимодействии тел ускорения получают оба взаимодействующих тела. На самом деле
и Луна влияет на Землю, заставляя её двигаться по окружности и сообщая ей
центростремительное ускорение. Но вокруг какого центра ?
Астрономические
наблюдения показали, что Луна обращается не вокруг центра Земли, а вокруг
некоторой точки Р,которая отстоит от центра Земли на 4700 км. (Эта точка находится внутри земного шара). Вокруг этой же точки Р движется по окружности центр Земли.
Значит, радиусы, соединяющие центры Земли и Луны с точкой Р, движутся с одинаковой угловой скоростью вокруг точки Р. Центр Земли движется по окружности радиусом
rз ≈ 4700 км,
а центр Луны – по окружности радиусом
rл ≈ 380 000 км.
Выходит, что Земля и Луна ведут себя совершенно так же, как алюминиевый и стальной цилиндр в центрифуге. Так как отношение центростремительных ускорений, сообщаемых цилиндрами друг другу, равно отношению радиусов окружностей, по которым они движутся. Точно так же отношение модулей ускорений Луны
и Земли
равно отношению радиусов rл и rз:
но отношение ускорений взаимодействующих тел равно обратному отношению их масс, поэтому
Так как
rл ≈ 380 000 км, а
Следовательно, масс Луны в 81 раз меньше массы Земли. Масса Земли была определена. Она равна 6 × 1024 кг. Тогда
Плотность вещества.
Для сравнения масс различных тел пользуются понятием плотности.
Каждое вещество занимает некоторый объём. И может оказаться, что объёмы
двух тел равны, а их массы различны. В этом случае говорят, что плотности этих
веществ различны.
Плотность вещества – это величина, измеряемая массой вещества в единице объёма.
Если масса тела m, а объём V, то плотность тела
где p – плотность вещества,
m – масса тела,
V – объём тела.
Полагая в этой формуле V = 1, получим p = m.
Из этого следует, что плотность вещества численно равна массе вещества,
содержащейся в единице объёма.
Массу тела по его плотности и объёму можно вычислить по формуле:
m = p × V.
Объём тела по его массе и плотности можно вычислить по формуле:
Чтобы лучше запомнить эти три формулы, их можно объединить в мнемонический треугольник:
Для нахождения любой из величин нужно мысленно закрыть буквенное обозначение этой величины, и получим формулу для её определения:
За единицу плотности вещества в системе СИ принимается
1 кг/м3,
а в системе СГС –
1
г/см3.
Плотность вещества в
г/см3, кг/дм3 и в т/м3
выражается одним и тем же числом, так
как увеличение числителя и знаменателя в
1000 раз не изменяет
отношения.
ПРИМЕР:
Рассмотрим кусок железа, масса которого равна 1 кг, и кусок дерева, масса которого равна 1 кг. Объём дерева больше, чем объём куска железа. Плотность дерева меньше, чем плотность железа (молекулы прилегают не так плотно друг к другу).
Плотность железа равна 7900 кг/м3,
Это означает, что масса 1 м3 железа равна 7900 кг.
Плотность воды равна 1000 кг/м3,
Это означает, что масса 1 м3 воды равна 1000 кг.
Выражаясь по-другому, плотность воды равна 1 г/см3, значит, масса 1 см3 воды равна 1 г.
В различных состояниях плотность вещества различна. Плотность веществ зависит от их состояния и температуры. При переходе в газообразное состояние плотность всех веществ уменьшается. При переходе из твёрдого состояния в жидкое плотность большинства веществ также уменьшается. Исключение: вода и лёд.
ПРИМЕР:
Плотность расплавленного железа меньше плотности твёрдого железа.
Плотность вещества зависит от атмосферного давления (строго говоря, от давления всех тел, включая атмосферный воздух). При увеличении давления плотность всех веществ возрастает.
ПРИМЕР:
В космосе плотность белого карлика Сириуса Б (звезда) так велика, что масса спичечного коробка из этого вещества была бы равна 127 тоннам.
Средняя плотность вещества – физическая величина, равная отношению массы тела к его объёму. Если тело однородное (состоит из одного вещества), то средняя плотность тела равна плотности его вещества.
ЗАДАЧА:
10 вёдер вместимостью 1 л до краёв наполнили мёдом, масса всего мёда равна 14 кг. Найдите плотность мёда.
РЕШЕНИЕ:
V = 10 л = 0,01 м3.
ОТВЕТ: Плотность мёда равна
ЗАДАЧА:
Латунь состоит из 65% меди и 35% цинка. Определите плотность сплава.
РЕШЕНИЕ:
Если масса латуни m, её объём V, то плотность латуни
Объём латуни V равен сумме объёма меди
и объёма цинка то есть Подставив значение объёмов в формулу для плотности ρ, получим
ОТВЕТ: ρ = 8,2 г/см3
ПРИМЕР:
Рассмотрим кусок железа, масса которого равна 1 кг, и кусок дерева, масса которого равна 1 кг. Объём дерева больше, чем объём куска железа. Плотность дерева меньше, чем плотность железа (молекулы прилегают не так плотно друг к другу).
Плотность железа равна 7900 кг/м3,
Это означает, что масса 1 м3 железа равна 7900 кг.
Плотность воды равна 1000 кг/м3,
Это означает, что масса 1 м3 воды равна 1000 кг.
Выражаясь по-другому, плотность воды равна 1 г/см3, значит, масса 1 см3 воды равна 1 г.
В различных состояниях плотность вещества различна. Плотность веществ зависит от их состояния и температуры. При переходе в газообразное состояние плотность всех веществ уменьшается. При переходе из твёрдого состояния в жидкое плотность большинства веществ также уменьшается. Исключение: вода и лёд.
ПРИМЕР:
Плотность расплавленного железа меньше плотности твёрдого железа.
Плотность вещества зависит от атмосферного давления (строго говоря, от давления всех тел, включая атмосферный воздух). При увеличении давления плотность всех веществ возрастает.
Плотность вещества зависит от температуры: при повышении температуры обычно
плотность снижается. Это связано с термическим расширением, когда при
неизменной массе увеличивается объём.
Плотности веществ могут быть различны. Самое плотное вещество не находится
на Земле.
ПРИМЕР:
В космосе плотность белого карлика Сириуса Б (звезда) так велика, что масса спичечного коробка из этого вещества была бы равна 127 тоннам.
Средняя плотность вещества – физическая величина, равная отношению массы тела к его объёму. Если тело однородное (состоит из одного вещества), то средняя плотность тела равна плотности его вещества.
ЗАДАЧА:
10 вёдер вместимостью 1 л до краёв наполнили мёдом, масса всего мёда равна 14 кг. Найдите плотность мёда.
РЕШЕНИЕ:
V = 10 л = 0,01 м3.
ОТВЕТ: Плотность мёда равна
ЗАДАЧА:
Латунь состоит из 65% меди и 35% цинка. Определите плотность сплава.
РЕШЕНИЕ:
Если масса латуни m, её объём V, то плотность латуни
Объём латуни V равен сумме объёма меди
и объёма цинка то есть Подставив значение объёмов в формулу для плотности ρ, получим
ОТВЕТ: ρ = 8,2 г/см3
Как, зная только массу, рассчитать плотность ?
– если объём тела (вещества) неизвестен или не задан явно в условии задачи, то надо его измерить,
вычислить или узнать, используя косвенные (дополнительные) данные;
– если вещество сыпучее или жидкое, то оно, как правило,
находится в ёмкости, которая обычно имеет стандартный объём; так, например,
объём бочки обычно равен 200 л, объём ведра – 10 л, объём стакана – 200 мл (0,2 л), объём столовой ложки – 20 мл, объём чайной – 5 мл; об объёме трёхлитровых и литровых банок
нетрудно догадаться из их названия;
– если жидкость занимает не всю ёмкость или ёмкость
нестандартная, то перелейте её в другую тару, объём которой известен; если подходящеё
ёмкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки); в процессе вычерпывания жидкости просто посчитайте количество таких
кружек и умножьте на объём мерной тары;
– если тело имеет простую форму, то вычислите его объём,
используя, соответствующие геометрические формулы; так, например,
если тело имеет форму прямоугольного параллелепипеда, то его объём будет равен
произведению длин его рёбер;
– если тело имеет сложную геометрическую форму, то
попробуйте (условно) разбить его на несколько простых частей,
найдите объём каждой из них отдельно и затем сложите полученные результаты;
– если тело невозможно разделить на более простые фигуры (например,
статуэтку), то воспользуйтесь
методикой Архимеда; опустите тело в
воду и измерьте объём вытесненной жидкости; если тело не тонет, то утопите его с помощью тонкой палочки (проволоки);
– если объём вытесненной телом воды посчитать
проблематично, то взвесьте вылившуюся воду, или найдите разность между
начальной и оставшейся массой воды; при этом, количество килограммов воды будет
равняться количеству литров, количество граммов – количеству миллилитров, а
количество тонн – количеству кубометров.



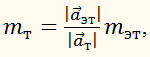

















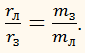











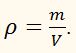





Комментариев нет:
Отправить комментарий