ВИДЕО УРОК
Выясним, какой величиной можно выразить силу, или, как говорят, какая
величина служит мерой силы, действующей на тело.
Очевидно, что эта величина должна быть одинаковой для всех тел, ускоряемых
одной и той же силой.
Найти такую величину можно только из опыта. Опыт должен состоять в том,
чтобы под действием одной и той же силы (безразлично, какой именно) привести в
ускоренное движение различные тела и найти величину, характеризующую ускоряемое
тело, которая одинакова для всех тел.
Для проведения опыта нужно выбрать тело, которое действует на все другие
тела с одинаковой силой. Таким телом может служить упруго деформированное тело,
например растянутая или сжатая пружина, в которой действует сила упругости
(опыт показывает, что других тел, обладающих таким свойством, в природе нет).
Сила упругости отличается от всех других сил той замечательной
особенностью, что она зависит только от взаимного расположения частей одного и
того же тела – растянутой пружины, а не взаимодействия её с другими телами.
Поэтому сила упругости растянутой пружины не изменится, когда к ней будет
прикреплено любое тело. На любое тело, прикреплённое к растянутой на
определённую длину пружине, действует одна и та же сила упругости пружины. Поэтому
опыт сводится к тому, чтобы тело, прикреплённое к пружине, привести в
ускоренное движение.
Удобнее всего, наблюдать за ускоренным движением тел по окружности, то есть
когда они движутся с центростремительным ускорением. Поэтому воспользуемся
центробежной машиной.
ОПЫТ:
Поместим тело М в виде алюминиевого цилиндра с просверленным по его оси отверстием на стержень центробежной машины.
Приведём машину во вращение. Тогда цилиндр М начнёт скользить по стержню, удаляясь от точки А и растягивая тем самым пружину. Не будь пружины, цилиндр дошёл бы до упора в точке В. Но вследствие силы упругости растянутой пружины цилиндр, удалившись несколько от оси вращения (на расстоянии х), станет двигаться по окружности радиусом r.
Центростремительное ускорение
цилиндра М направлено по радиусу к центру. Вдоль радиуса
направлена и ось пружины. Следовательно, ускорение цилиндра М направлено вдоль оси пружины так же, как и
сила упругости. Ясно, что эта сила и сообщает цилиндру центростремительное
ускорение.
Центростремительное
ускорение по абсолютному значению равно:где ω – угловая скорость вращения машины. Измерив угловую скорость ω и радиус r, найдём модуль ускорения
Заменим теперь алюминиевый цилиндр точно таким же по размерам стальным цилиндром, массой в три раза большей. Приведём машину снова во вращение и подберём такую скорость этого вращения, чтобы растяжение пружины было таким же, каким оно было при вращении цилиндра из алюминия. Тогда и сила, действующая на стальной цилиндр, будет такой же.
Опыт показывает, что в этом случае угловая скорость вращения машины будет в √͞͞͞͞͞3 раз меньше. Это значит, что ускорение стального цилиндра в 3 раза меньше, чем алюминиевого. Направлено это ускорение по-прежнему вдоль оси пружины (по радиусу окружности к центру). Выходит, что при увеличении массы тела втрое, ускорение, сообщаемое телу одной и той же силой, сохраняет своё направление, а по абсолютному значению уменьшается в 3 раза.
Отсюда следует, что произведение
массы тела на его ускорение для обоих тел одно и то же.
Можно провести этот опыт со множеством других тел самых различных масс. Он покажет, что при одном и том же растяжении пружины, то есть при одной и той же силе, произведение массы тела на его ускорение для всех тел одно и то же.
Мы нашли величину, одинаковую для различных тел, на которые действует одна
и та же сила. Значит, произведение массы тела на его ускорение выражает силу,
действующую на тело.
Если обозначить силу,
действующую на тело, черезускорение тела через
а его массу через m, то можно написать:
Но, может быть, это верно только для силы упругости растянутой пружины и к другим силам не относится ? Чтобы ответить на этот вопрос, проведём ещё один опыт.
ОПЫТ:
Возьмём ту же пружину, но расположим её вертикально, закрепив верхний конец неподвижно.
К нижнему концу пружины подвесим груз известной массы m.
Мы увидим, что пружина растянется, а груз будет находиться в покое (после нескольких колебаний).
На груз теперь действуют одновременно две силы: сила тяжести со стороны Земли и сила упругости со стороны растянутой пружины. Не будь пружины, груз под влиянием Земли падал бы свободно вниз с ускорением
направленным по вертикали вниз. Но ускорение груза равно нулю. Это означает, что растянутая пружина сама по себе тоже сообщила бы грузу ускорение
(направленное вертикально вверх). Значит, сила тяжести
и сила упругости
действующие на груз, равны по абсолютному значению и противоположны по направлению: Но сила упругости, действующая на тело, как мы только что выяснили, равна произведению массы на ускорение, которое она ему сообщает, то есть Значит, сила тяжести равная будет равна: Так мы установили, что сила тяжести тоже равна произведению массы тела на ускорение, сообщаемое ему этой силой.
Опыты, подобные рассмотренным выше, и многие другие позволили Ньютону
сформулировать один из важнейших законов механики – второй закон Ньютона.
сформулировать один из важнейших законов механики – второй закон Ньютона.
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.
Математически второй закон Ньютона выражается формулой
Во всех опытах скорости и ускорения измерялись относительно инерциальной системы отсчёта. Следовательно, второй закон Ньютона справедлив только в инерциальных системах отсчёта.
Из второго закона Ньютона следует, что действующие на
тело силы определяют его ускорение, то есть изменение скорости,
а не саму скорость движения тела. Поэтому направление
ускорения всегда совпадает с направлением действующей силы.
Направление же скорости, а следовательно, и перемещения может и не совпадать с
направлением действующей силы. Так, например, сила может быть всё время
направлена перпендикулярно скорости движения тела. В этом случае движение
происходит по окружности, а ускорение, так же как и сила, направлено по
радиусу, поведенному от движущегося тела к центру. Так двигалось тело под
действием силы упругости в центробежной машине.
Если тело
взаимодействует не с одним, а с несколькими телами, то на него действует не
одна, а несколько сил, причём силы <<не мешают>> друг другу
сообщать телу, на которое они действуют, своё ускорение. Поэтому ускорение,
которое сообщает телу все совместно действующие на него силы, будет такое же,
какое сообщала бы ему одна сила, равная сумме всех этих сил. Так как сила –
величина векторная, то под суммой всех сил
надо понимать векторную сумму. Такая сумма называется равнодействующей всех приложенных к телу
сил. И в формулевыражающей второй закон Ньютона, под
нужно понимать равнодействующую всех сил, действующих на тело.
ПРИМЕР:
На качелях, известных под названием <<гигантские шаги>>, на человека действуют одновременно две силы:
сила
– со стороны Земли, направленная вниз, и сила
– со стороны каната, направленная вдоль каната. Под действием двух сил <<пассажир>> движется по окружности вокруг столба, к которому прикреплён канат. Значит, ускорение направлено к центру окружности, а не вдоль силы
Из рисунка видно, что к центру окружности направлена и сила
которая равна геометрической сумме сил <<Пассажир>>, следовательно, движется так, как будто бы на него действуют не две силы: а всего одна – их равнодействующая Векторная сумма сил, действующих на тело, может быть равна и нулю. Тогда ускорение тела тоже будет равно нулю, и тело будет либо покоиться, либо двигаться прямолинейно и равномерно.
ПРИМЕР:
В подвешенном на шнуре шарике компенсация тел состоит в том, что силы, с которыми на шарик действуют шнур и Земля, противоположны по направлению и равны по абсолютному значению
поэтому их равнодействующая равна нулю.
На рисунке
Показан случай, когда нулю равна равнодействующая, то есть векторная сумма, не двух, а трёх сил:
действующих на тело (фонарь).
Пользуясь понятием силы, можно дать другую формулировку первого закона
Ньютона.
Существуют системы отсчёта, относительно которых тело
движется прямолинейно и равномерно или находится в покое, если равнодействующая
всех сил, действующих на тело, равна нулю.
Из формулы
выражающей второй закон Ньютона, видно, в каких единицах измеряется сила.
Сила, равна единице, если, действуя на тело, масса
которого равна единице, она сообщит ему ускорение, равное единице.
В СИ за единицу силы принимается сила, которая телу
массой 1 кг сообщает
ускорение 1 м/cек2. Эту единицу называют ньютоном (сокращенно: Н):
В системе СГС за единицу силы
принимается сила, в 105 раз меньшая
ньютона. Она сообщает телу массой 1 г ускорение
1 см/сек2.
Эту единицу силы называют диной.
1 Н = 105 дин.
ПРИМЕР:
Сила тяжести, действующая на
тело массой 1 кг, вблизи поверхности Земли равна:
F = 1 кг × 9,8 м/сек2 =
9,8 Н = 9,8 × 105 дин.ЗАДАЧА:
К концам нити, перекинутой
через укреплённый неподвижный блок, подвешены грузы массами m1 = 95 г и m2 = 105 г. Более тяжёлый груз вначале поднят в верхнее положение,
а затем отпущен. Определить, на каком расстоянии от верхнего положения будет
находиться тяжёлый груз через t = 2 сек
?
РЕШЕНИЕ:
Освобождённый груз массой m2 придёт в равноускоренное движение; одновременно с ним придёт в равноускоренное движение груз массой m1. Грузы начали движение из состояния покоя, поэтому путь, пройденный грузом (одним – вверх, а другим – вниз), определяется по формуле пути равноускоренного движения без начальной скорости, то есть по формуле:
Ускорение а, по второму закону Ньютона, равно
где F – сила, равная разности весов гирь, то есть
F = P2 – P1 = (m2 – m1)g,
а m = m2 + m1 – масса движущейся системы, тогда
Искомое расстояние:
ОТВЕТ: h = 0,98 м
Если при решении
подобных задач в числитель и знаменатель или в правую и левую части равенства
входят в качестве множителей величины одного наименования в одной и той же
степени, то их можно не переводить в ту систему единиц, в которой решается
задача, а брать в любых, но одинаковых единицах, так как их наименования
взаимно сократятся.





























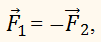










Комментариев нет:
Отправить комментарий