Функція
зростає.
Найпростішими логарифмічними нерівностями називають нерівності вигляду
logа
х > b або logа х < b.
Перша з них має множину розв'язків:
х > ab при
а > 1,
0 < х < ab
при 0 < а < 1.
ПРИКЛАД:
Розв'язати
нерівність:
log2 (х –5) > 3.
ОДЗ:
х – 5 > 0, тобто х > 5.
log2 (х –5) > log2 23.
Функція log2 t є
зростаючою, отже,
х
– 5 > 23, х > 13.
Ураховуючи ОДЗ, маємо
х > 13.
ВІДПОВІДЬ:
(13; +∞).
ПРИКЛАД:
Розв'язати
нерівність:
5 < х < 51/8.
ВІДПОВІДЬ:
(5; 51/8).
ПРИКЛАД:
Розв'язати
нерівність:
log0,5 х
≥ 3.
Потенціюючи
вихідну нерівність, маємо:
х
≤ 0,53, 0 < х ≤ 0,125.
ПРИКЛАД:
Розв'язати
нерівність:
Звідки
0 < lg
х(1
– lg
х) < 1.
Як
бачимо, розв'язок х мусить задовольняти дві нерівності:
lg2 х
– lg
х
+ 1 > 0 і
lg х(1 – lg
х) > 0.
Першу
задовольняє будь-яке додатне значення х,
тому що дискримінант тричлена в його лівій частині від’ємний. Другу
задовольняють значення х,
при яких
0 < lg
х < 1,
тобто
0 < х < 10.
Завдання до уроку 8
Інші уроки:


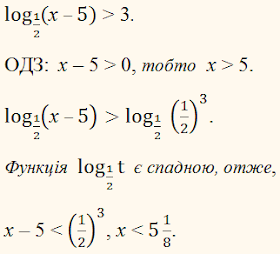


Комментариев нет:
Отправить комментарий