Урок 3. Сложение и вычитание векторов

ВИДЕО УРОК

Первой операцией над векторами является сложение векторов.

Если материальная точка переместилась из точки  А  в точку  В, а потом из точки  В  в точку  С, то в результате она перейдёт из точки  А  в точку  С.

Поэтому говорят, что направленные отрезки

характеризующие эти перемещения, складываясь, дают направленный отрезок

Это записывают так:

В этом случае видно, что процесс сложения векторов происходит так:

конец первого вектора

является началом второго

а суммарный вектор

соединяет начало первого вектора и конец второго.

Правило треугольника.

Чтобы найти сумму двух векторов

нужно:

– отложить вектор

равный

от произвольной точки  С;

– отложить вектор

равный  b, от точки  D;


– построить вектор

который соединяет начало первого слагаемого с концом второго;


– вектор

является суммой векторов

ПРИМЕР:

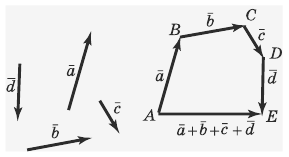
На рисунке

изображены:

ПРИМЕР:

На рисунке

изображены:

ПРИМЕР:

Пусть, двигаясь горизонтально со скоростью  3 м/сек, кран поднимает ящик со скоростью  1 м/сек. На рисунке

 изображены в масштабе скорость ящика относительно крана

направленная вертикально вверх, и скорость движения крана

направление которой совпадает с направлением движения крана.

Сумма векторов

– вектор

который изображает скорость ящика относительно неподвижной системы отсчёта:

Чтобы сложить эти векторы, нужно:

1. Выбрать исходную точку  А  (возможно, ту точчку, к которой приложена заданная сила).

2. От точки  А  отложить вектор

3. От точки  В  отложить вектор

4. Построить вектор

Правило параллелограмма для сложения неколлинеарных векторов.

ПРИМЕР:

Пусть нам даны векторы

которые неколлинеарны, то есть не лежат на одной прямой.

Отложим эти векторы от некоторой точки  А, то есть

Тогда суммарный вектор изобразится диагональю параллелограмма АВСD, построенного на векторах

Мы получили второе правило сложения векторов – правило параллелограмма.

Если векторы неколлинеарные, то их сумма представляется диагональю построенного на них параллелограмма.

Чтобы найти сумму двух неколлинеарных векторов

нужно:

– отложить от произвольной точки  О  векторы

– использовать эти векторы как стороны параллелограмма;

– построить вектор

– диагональ параллелограмма, соединяющую вершины  О  и  С:

искомый вектор – сумма векторов

Для любого вектора

верно равенство

Законы сложения векторов. 

Переместительный закон:

Сочетательный закон:

Эти равенства справедливы для любых векторов

Правило многоугольника.

Для того, чтобы сложить любое количество векторов, надо последовательно откладывать эти векторы таким образом, чтобы каждый следующий вектор начинался от конца предыдущего. Тогда суммой всех данных векторов будет вектор, который начинается от начала первого вектора и соединяет его с концом последнего. Порядок сложения значения не имеет.

ПРИМЕР:

Чтобы сложить несколько векторов, например векторы

удобно построить векторную ломаную.

Эта ломаная состоит из направленных отрезков

Вектор

соединяющий начало ломаной  ABCD  и её конец, и является суммой

Если ломаная получилась замкнутой, то сумма векторов равна нуль-вектору,

то есть

Для любого вектора

выполняется равенство

ПРИМЕР:

На рисунке

изображена сумма

Можно складывать в другом порядке:

Результат при этом будет тот же.

Нахождение суммы векторов с помощью координат.

При сложении векторов их соответствующие координаты складываются. А именно, если

то есть

ПРИМЕР:

Найти сумму векторов:

РЕШЕНИЕ:

Разложение вектора на составляющие.

При изучении и использовании векторов часто приходится говорить о так называемом разложении вектора на составляющие.

Составляющими данного вектора называют такие векторы, сумма которых равна этому вектору.

Данный вектор <<составляется>> из составляющих как сумма слагаемых и разлагается на них как на слагаемые, поэтому говорят о разложении на составляющие.

Пусть в плоскости  α  даны две прямые  а  и  b, пересекающиеся в точке  О. Возьмём какой-нибудь вектор

и отложим его от точки  О.

Если точка  V  не лежит ни на прямой  а, ни на прямой  b, то проведём через точку  V  прямые

и построим параллелограмм  OAVB. Его диагональю будет отрезок  OV, а его стороны  ОА  и  ОВ  лежат соответственно на прямых  а  и  b. По правилу параллелограмма для сложения векторов получим

Векторы

являются составляющими вектора

по прямым  а  и  b,

Если  V ∈ a, то

а составляющая по  b  нулевая:

Аналогично в случае, когда

Мы выполнили разложение вектора по двум пересекающимся прямым.

Можно разложить вектор по двум неколлинеарным векторам.

Возьмём два неколлинеарных вектора

Отложим их от точки  О.

Пусть

– вектор параллельный плоскости  ОВС. Отложим его от точки  О.

Через точку  А  проведём прямые, параллельные векторам

Тогда

Векторы

коллинеарны.
Значит,

и поэтому

Такое представление вектора

через векторы

называют разложение вектора по неколлинеарным векторам.

Разность векторов.

Введём операцию разности двух векторов. Эта операция вводится так же как и для чисел.

Разностью векторов

называют такой вектор

который в сумме с вычитаемым вектором

даёт вектор

Разностью векторов

будет вектор

то есть вектор, который соединяет концы векторов

и направлен от вычитаемого к уменьшаемому.

ПРИМЕР:

Построим разность двух векторов

Отложим от какой-нибудь точки  О  данные векторы

Рассмотрим вектор

Мы видим, что

(правило треугольника).
Вектор

будет разностью векторов

то есть

Если вектор

обозначить через

Равенство

можно назвать правилом нахождения разности двух векторов.

Противоположные векторы – векторы, имеющие одинаковые длины и противоположно направленные.

На рисунке

 изображены два противоположных друг другу вектора.

Записывают их так:

Причём, если сложить противоположные векторы (по правилу треугольника), то в сумме получится нуль-вектор, то есть:

Верно и обратное утверждение: если сумма двух векторов равна нуль-вектору, то они противоположны.

Если

Нуль-вектор считается противоположным самому себе.

Определение разности векторов с помощью координат.

Координаты разности двух векторов равняются разности соответствующих координат вектора – уменьшаемого и вектора – вычитаемого.

Теорема о разности векторов.

Равенство

справедливо для любых векторов

Правила вычитания векторов.

ПЕРВЫЙ СПОСОБ

Для того чтобы вычесть из одного вектора другой, надо к первому вектору прибавить вектор, противоположный второму.

ПРИМЕР:

ВТОРОЙ СПОСОБ

Для того чтобы вычесть из одного вектора другой, надо из произвольной точки плоскости отложить оба вектора, затем построить вектор, который начинается на конце второго вектора (вычитаемого), а заканчивается на конце первого вектора (уменьшаемого).

ПРИМЕР:

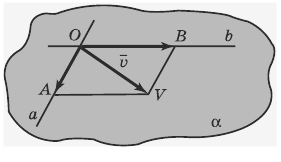
ПРИМЕР:

Пусть даны векторы

Построить вектор

РЕШЕНИЕ:

Построим произвольную точку  О  и отложим от неё векторы

Соединив точку  В  с точкой  А, получим вектор

По правилу треугольника для построения суммы двух векторов видим, что

то есть

тогда

ОТВЕТ:

ПРИМЕР:

Пусть

Найдите  вектор:

РЕШЕНИЕ:

ОТВЕТ:

Задания к уроку 3

• Задание 1
• Задание 2
• Задание 3

ДРУГИЕ УРОКИ

• Урок 1. Понятие вектора
• Урок 2. Координаты вектора
• Урок 4. Произведение векторов
• Урок 5. Векторы в пространстве
• Урок 6. Действия над векторами в пространстве
• Урок 7. Решение задач с помощью векторов
• Урок 8. Преобразование фигур