Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
ФОРМУЛИ ПОЛОВИННОГО АРГУМЕНТУ
або
ВІДЕО УРОКОМ
1. Обчислите:
ctg 15°.
а) 2 – √͞͞͞͞͞3;
б) 2 + √͞͞͞͞͞2;
в) 2 + √͞͞͞͞͞3
;
г) 2 – √͞͞͞͞͞2.
2.
Обчислите:
(2 + √͞͞͞͞͞2) sin2 π/8.
а) 0,5;
б) 1,5;
в) 0,1;
г) 1.
3.
Знайдіть:
sin 4α + соs 4α сtg 2α,
якщо tg 2α = 4.
а) 1/2;
б) 3/4;
в) 3/2;
г) 1/4.
4. Знайдіть tg α,
якщо
cos 2α = –5/13 і α
∈ (π; 3/2π).
а) 1;
б) 1,5;
в) 1,8;
г) 0,5.
5. Знайдіть соs α, якщо tg α/2 = 2.
а) 0,6;
б) –0,8;
в) –0,6;
г) 0,8.
6. Обчисліть, не
користуючись калькулятором або таблицями:
tg 5π/8.
а) √͞͞͞͞͞2
– 1;
б) –√͞͞͞͞͞3
– 1;
в) –√͞͞͞͞͞2
– 1;
г) √͞͞͞͞͞3
– 1.
7. Спростіть вираз:
2 cos2(π/4 – x/2).
б) 1
– sin x;
в) 1 – 2 sin x;
г) 1 + sin x.
8.
Спростіть вираз:
2 sin2(π/4 – x/2).
а) 1
– 2 sin x;
б) 1 +
sin x;
в) 1
– sin x;
г) 1 +
2sin x.
9. Спростіть вираз:
а) sin2 2α при 2πk < α < π + 2πk, k ∈ Z, –(1 + соs2 α) при –π + 2πk < α
< 2πk, k
∈ Z;
б) sin2
α при 2πk
< α < π + 2πk, k
∈ Z,
–(1 + соs2 α) при –π + 2πk < α
< 2πk, k
∈ Z;
в) sin2
2α при 2πk < α < π +
2πk, k
∈ Z,
–(1 – соs2 α) при –π + 2πk < α
< 2πk, k
∈ Z;
г) sin2
α при 2πk
< α < π + 2πk, k
∈ Z,
–(1 – соs2 α) при –π + 2πk < α
< 2πk, k
∈ Z.
–(1 – sin2
α) при –π + 2πk < α
< 2πk, k
∈ Z;
б) cos2
α при 2πk
< α < π + 2πk, k
∈ Z,
–(1 – sin2
α) при –π + 2πk < α
< 2πk, k
∈ Z;
в) cos2
2α при 2πk < α < π +
2πk, k
∈ Z,
–(1 + sin2
α) при –π + 2πk < α
< 2πk, k
∈ Z;
г) cos2
α при 2πk
< α < π + 2πk, k
∈ Z,
–(1 + sin2
α) при –π + 2πk < α
< 2πk, k
∈ Z.
11. Спростіть вираз:
б) sin x;
в) cos x;
г) sin 2x.
б) cos x;
в) sin 2x;

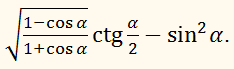


Комментариев нет:
Отправить комментарий