Уроки математики и физики для школьников и родителей: Урок 7. Ускорение

ВИДЕО УРОК

Равноускоренное движение.

При неравномерном движении мгновенная скорость тела непрерывно изменяется: от точки к точке, от одного момента времени к другому. Как же вычислить скорость в любой момент времени ? Для этого нужно знать, как быстро изменяется скорость, или, другими словами, каково её изменение в её изменение в единицу времени. Для простоты мы будем рассматривать такое неравномерное движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково. Такое движение называется равноускоренным.

Движение, при котором скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным движением.

Ускорение.

Если в некоторый начальный момент времени скорость тела равна

а через промежуток времени t она оказывается равной

то за каждую единицу времени скорость изменяется на

Величина

характеризует быстроту измерения скорости. Её называют ускорением и обозначают буквой а:

Ускорением движущегося тела называют величину, равную отношению изменения скорости тела к промежутку времени, в течении которого это изменение произошло.

Если ускорение тела по абсолютному значению велико, то это значит, что оно быстро набирает скорость (когда тело разгоняется) или быстро теряет его (при торможении).

Если ускорение

известно, то можно вычислить значение скорости

тела в любой момент времени, если известно ещё и значение начальной скорости

Из формулы

следует, что

Ускорение и нужно знать для вычисления скорости

Так как ускорение равно произведению векторной величины

на скаляро

но само является векторной величиной.

В каких единицах измеряют ускорение ?

Так как

то абсолютное значение ускорения равно единице, если равно единице абсолютное значение изменения скорости и равен единице промежуток времени.

Положив в формуле ускорения v – v₀ = 1 м/сек и t = 1 сек, получим единицу ускорения в системе СИ:

т. е. за единицу ускорения в системе СИ принимается ускорение такого равнопеременного движения, при котором за каждую секунду скорость изменяется на 1 м/сек. Наименование единицы ускорения читается так: <<метр в секунду за секунду>>, или <<метр, деленный на секунду в квадрате>>. В системе СГС за единицу ускорения принимают 1 cм/сек².

За единицу ускорения принимают ускорение такого движения, при котором за единицу времени скорость изменяется на единицу скорости.

В системе единиц СИ скорость измеряется в метрах в секунду, а время – в секундах, так что ускорение измеряется в метрах в секунду за секунду или в метрах на секунду в квадрате (м/сек²). В системе единиц СГС скорость измеряется в см/сек, а время в секундах, поэтому единицей ускорения является 1 см/сек².

Направление ускорения.

При прямолинейном движении векторы

направлены вдоль одной прямой, которая является в то же время и траекторией движения. Вдоль этой же прямой в направлении движения тела мы условились направлять и координатную ось (ось Х). В таком случае вектор разности

а значит и вектор ускорения

лежит на той же прямой. Но куда он направлен – в сторону движения (так же как ось Х) или против него ?

Проекция разности двух векторов на какую-нибудь ось равна разности из проекций на ту же ось. Следовательно, для проекций векторов

на ось Х можно написать

Здесь а – проекция вектора

на ось Х; v и v₀ – проекция векторов

на туже ось.

Так как все три вектора лежат на одной прямой (оси Х), то абсолютные значения их проекций равны абсолютным значениям самих векторов.

Рассмотрим 2 случая ускоренного движения тела.

ПЕРВЫЙ СЛУЧАЙ

Скорость тела по абсолютному значению растёт (тело <<разгоняется>>). Это значит, что v ˃ v₀. Тогда из формулы

видно, что проекция ускорения а положительна и равна

Вектор

Следовательно, направлен так же, как ось Х, т. е. в сторону движения.

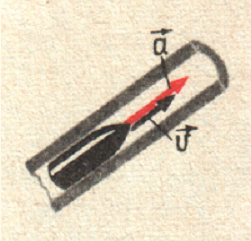
ПРИМЕР:

Когда бронебойный снаряд движется при выстреле в стволе орудия, его скорость растёт и ускорение направлено так же, как и скорость.

ВТОРОЙ СЛУЧАЙ

Тело тормозится, т. е. абсолютное значение его скорости уменьшается

Из формулы

видно, что проекция ускорения

в этом случае, отрицательна:

Из формулы

можно получить выражение для скорости v:

v = v₀ + at.

В этой формуле

v, v₀ и a – проекции векторов

на ось Х, которые могут быть как положительными, так и отрицательными.

При решении задач выражение для скорости

v = v₀ + at

удобно записать так, чтобы из него сразу было видно, как направлен вектор ускорения.

Если скорость тела растёт (разгон), то

Когда же скорость тела уменьшается (торможение),

Понятно, что тело, которое тормозится, должно когда-то остановиться. Это произойдёт, как это видно из формулы

тогда, когда

станет равным v₀, т. е. в момент времени

Но если ускорение остаётся постоянным (по модулю и направлению) и после этого момента, то тело, остановившись, начнёт двигаться в противоположную сторону. Это видно из того, что при

величина

станет больше, чем v₀; скорость v изменит свой знак на обратный. Так движется тело, брошенное вертикально вверх: долетев до высшей точки траектории, тело начинает движение вниз.

Если v₀ = 0 и вектор ускорения направлен также, как и ось координат, то из формулы

следует, что

Если же ось координат выбрана так, что направление вектора ускорения противоположно направлению оси координат, то из формулы

следует, что

Знак <<–>> в этой формуле означает, что вектор скорости, так же как и вектор ускорения, направлен противоположно направлению оси координат. Модуль скорости, конечно, и в этом случае увеличивается со временем.

Обычно называют движение с возрастающей по абсолютной величине скоростью ускоренным движением, а движение с убывающей скоростью – замедленным движением.
Но в механике любое неравномерное движение является ускоренным движением. Трогается ли автомобиль с места или тормозит, в обоих случаях он движется с ускорением. Ускоренное прямолинейное движение отличается от замедленного только знаком проекции вектора ускорения.

Перемещение, скорость и траектория движения различны относительно разных тел отсчёта, движущихся друг относительно друга.

А ускорение ? Относительно ли оно ?

Ускорение тела определяется векторной разностью двух значений его скорости в различные моменты времени. При переходе от одной системы координат к другой, движущейся относительно первой равномерно и прямолинейно, изменятся оба значения скорости. Но изменяются они на одну и ту же величину. Разность же их останется неизменной. Поэтому и ускорение останется неизменным.

Во всех системах отсчёта, движущихся друг относительно друга прямолинейно и равномерно, ускорение тела одинаково.

Но ускорения тела будут различными в системах отсчёта, движущихся с ускорением друг относительно друга. В этом случае ускорения складываются так же как скорости.

ЗАДАЧА:

Автомобиль проезжает мимо наблюдателя, двигаясь со скоростью 10 м/сек. В этот момент водитель нажимает на тормоз, и автомобиль начинает двигаться с ускорением 1 м/сек². Сколько времени пройдёт с того момента, когда водитель нажал на тормоз, до остановки автомобиля ?

РЕШЕНИЕ:

Выберем за начало отсчёта то место, в котором находится наблюдатель, и направим координатную ось в сторону движения автомобиля. Тогда проекция скорости автомобиля на эту ось будет положительной. Так как скорость автомобиля уменьшается, то проекция ускорения отрицательна и мы должны воспользоваться формулой:

Откуда

Подставляя в эту формулу численные значения заданных величин, получим:

За положительное направление координатной оси можно принять и направление, противоположное движению. Тогда проекция начальной скорости автомобиля будет отрицательной (v₀ = –10 м/сек), а проекция ускорения – положительной, и применять тогда нужно формулу:

Отсюда

Результат получился тот же.

Измерение ускорения.

Простейший способ измерения ускорения состоит в следующем. На тело, движущееся равноускоренно, помещают капельницу, т. е. сосуд с окрашенной жидкостью, из которого через определённые равные промежутки времени вытекают капли.

Падающие капли указывают положение тела через одинаковые и известные промежутки времени, которые мы обозначим буквой τ. Разность расстояний между упавшими каплями за два любых следующих друг за другом промежутка времени τ равна aτ², где а – ускорение. Измерив длины l₁ и l₂ двух соседних промежутков между каплями, мы и найдём ускорение по формуле

l₂ – l₁ = aτ²,

откуда

Часто пользуются другим, более точным способом. Это так называемый стробоскопический метод. Он состоит в том, что движущееся тело в темноте освещают через равные промежутки времени световой вспышкой. Ясно, что тело будет видно только в тех положениях, в которых оно оказывается освещённым. Если тело в процессе его движения фотографировать (затвор фотоаппарата должен быть открыт в течении всего времени движения), то на фотографической плёнке будут видны последовательные положения тела через равные промежутки времени. Измеряя расстояния между изображениями тела на плёнке и зная промежутки времени между световыми вспышками, можно вычислить ускорение, если известен масштаб изображения. Рисунок

представляет собой копию с фотографии падающего шара, полученной методом вспышек. Рядом помещена шкала для измерения расстояния.

Следует заметить, что изучение прямолинейного равноускоренного движения несколько затруднительно из-за того, что движущееся тело довольно быстро удаляется от наблюдателя. Так, например, для шарика, на фотографии