Урок 11. Нерівність з модулем

ВИДЕО УРОК

Щоб вирішити нерівність, що містить змінну під знаком модуля, треба звільнитися від знака модуля, використовуючи його визначення:

На практиці це робиться так:

1) знаходять критичні точки, тобто значення змінної, при яких вирази, що стоять під знаком модуля, звертаються в нуль;

2) розбивають область допустимих значень змінної на проміжки, на кожному з яких вирази, що стоять під знаком модуля, зберігають знак;

3) на кожному з знайдених проміжків вирішують нерівність без знака модуля.

Сукупність (об'єднання) рішень зазначених проміжків і становить всі рішення розглянутого нерівності.

Розглянемо нерівність 

Іноді корисно скористатися геометричною інтерпретацією модуля дійсного числа, згідно якої

|а|

означає відстань точки  а  координатній прямій від початку відліку  0, а

|а – b|

означає відстань між точками  а  і  b  на координатній прямій.

Розглянемо нерівність 

|x| < а, де  а > 0.

|x| < а, де  а > 0.

Скористаємося геометричною інтерпретацією модуля числа.

Нерівність виду  |x| < а  задовольняють  координати тих і тільки тих точок координатної прямої, які віддалені від початку відліку на відстань, меншу ніж  а, тобто 

–а < x < а,  х ∈ (–а, а).

Якщо ж  а ≤ 0, то дана нерівність розв'язків не має.

Крім того, можна використати метод зведення в квадрат обох частин нерівності.

Якщо вирази  f(x)  і  g(x)  при будь-яких  х  набувають тільки ненегативних значень, то нерівності

f(x) ˃ g(x) и

(f(x))² ˃ (g(x))²

рівносильні.

Застосовується ця теорема при рішенні нерівностей з модулем так.

Нехай треба вирішити нерівність

| f(x)| ˃ |g(x)|.

Оскільки при будь-яких  х  з області визначення виразів

f(x)  і  g(x)

справедливі співвідношення

| f(x)| ≥ 0, |g(x)| ≥ 0,

(| f(x)|)² = (f (x))²,

(|g(x)|)² = (g(x))²,

та ця нерівність рівносильно нерівності

(f(x))² ˃ (g(x))².

ПРИКЛАД:

Розв’яжіть нерівність:     

|x + 1| < |x – 3|.

РОЗВ'ЯЗАННЯ:

Перший спосіб.

Оскільки обидві частини нерівності ненегативні, то при зведенні їх в квадрат отримуємо рівносильну нерівність:

х² + 2х + 1 < х² – 6х + 9.

Ця нерівність рівносильна нерівності

8х < 8,

звідки  х < 1.

ВІДПОВІДЬ:  х < 1

Другий спосіб.

Рішення цієї нерівності зводиться до знаходження точок  х  числової прямої, які розташовані ближче до точки  –1, чим до точки  3.

Такими точками є усі точки, що лежать зліва від точки  1, - середини відрізку  [–1; 3], тобто точки з проміжку

(–∞; 1).

Третій спосіб.

Побудуємо графіки функцій

у = |x + 1|,

у = |x – 3|.

Ці графіки перетинаються в точці  (1; 2). При  х < 1  графік функції

у = |x + 1|

лежить нижче графіку функції

у = |x – 3|,

а при  х ˃ 1 – вище. Тому безліч рішень цієї нерівності – проміжок

(–∞; 1).

ПРИКЛАД:

Розв'яжіть нерівність:     

|x + 4| ≥ 1.

РОЗВ'ЯЗАННЯ:

Критична точка знаходиться рішенням рівняння

х + 4 = 0,

звідки

х = –4.

1) Розглянемо проміжок  х < –4. На ньому вихідне нерівність приймає вигляд 

–х – 4 ≥ 1.

Вирішуючи цю нерівність, знайдемо  х ≤ –5.

Так як

х < –4  и  х ≤ –5,

То рішенням вихідного нерівності буде проміжок

х ≤ –5.

2) Розглянемо проміжок  х ˃ –4. На ньому вихідне нерівність має вид

x + 4 ≥ 1,

Звідки

x ≥ –3.

Так як

х ˃ –4  і  x ≥ –3,

То рішенням вихідного нерівності буде проміжок

x ≥ –3.

3) З огляду на випадки  1)  і  2), остаточно маємо

х ≤ –5  і  x ≥ –3.

ВІДПОВІДЬ:

х ≤ –5  і  x ≥ –3

ПРИКЛАД:

Розв'яжіть нерівність:     

|x – 3| < 1.

РОЗВ'ЯЗАННЯ:

Знайдемо критичну точку

х – 3 = 0, тобто  х = 3.

1) Розглянемо проміжок  х < 3. В цьому випадку маємо

звідки

Отже рішенням вихідного нерівності є проміжок

(2; 3).

2) Розглянемо проміжок  х ≥ 3. В цьому випадку маємо

або

Отже рішенням вихідного нерівності є проміжок

[3; 4).

3) Розглянемо разом ці проміжки. Рішенням нерівності буде проміжок

(2; 4).

ВІДПОВІДЬ:

2 < x < 4.

ПРИКЛАД:

Розв'яжіть нерівність:     

|2x – 1| – |x – 2| ≥ 4.

РОЗВ'ЯЗАННЯ:

Критичними точками є

х = ¹/₂  і  х = 2.

1) Розглянемо проміжок  х < ¹/₂. На ньому вихідне нерівність має вид

–2х + 1 – (–х + 2) ≥ 4,

звідки  х ≤ –5. Отже, на цьому проміжку рішенням нерівності буде проміжок  х ≤ –5.

2) Розглянемо проміжок

¹/₂ ≤ х < 2.

На ньому вихідне нерівність має вид

3) Розглянемо проміжок  х ˃ 2. На ньому вихідне нерівність має вид

(2х – 1) – (х – 2) ≥ 4,

звідки  х ≥ 3.

4) Об'єднання отриманих рішень

х ≤ –5  і  х ≥ 3

буде вирішенням вихідного нерівності.

ВІДПОВІДЬ:

–∞ < х ≤ –5  и  3 ≤ х < +∞.

ПРИКЛАД:

Розв'яжіть нерівність:

|4x – 5| > 7.

Задана нерівність рівносильна сукупності нерівностей

звідки

ВІДПОВІДЬ: 

(–∞; –0,5) ∪ (3; +∞)

ПРИКЛАД:

Розв’яжіть нерівність:     

|x – 1| < 2.

РОЗВ'ЯЗАННЯ:

Перший спосіб.

|x – 1| можна розглядати як відстань на координатній прямій між точками  х  і  1. Значить, нам треба вказати на координатній прямій усі точки  х, які віддалені від точки  1  менше ніж на  2 одиниці. За допомогою координатної прямої

встановлюємо, що безліч рішень нерівності буде інтервал  (–1; 3).

Другий спосіб.

Звівши обидві частини цієї нерівності в квадрат, отримаємо рівносильну йому нерівність

(х – 1)² < 4.

Вирішуючи останню нерівність, отримаємо:

х² – 2х – 3 < 0,

звідки знаходимо, що

–1 < х < 3.

Третій спосіб.

За визначенням модуля числа,

тому цю нерівність можна замінити сукупністю двох систем нерівностей:

З першої системи отримуємо

1 ≤ х < 3.

З другої системи

–1 < х < 1.

Об'єднавши ці рішення, отримаємо проміжок

(–1; 3).

ВІДПОВІДЬ:  (–1; 3)

ПРИКЛАД:

Розв’яжіть нерівність:     

|2x + 5| ≥ 7.

РОЗВ'ЯЗАННЯ:

Перетворимо нерівність таким чином:

|x + 2,5| ≥ 3,5.

Вкажемо на координатній прямій усі такі точки  х, які віддалені від точки  –2,5  на відстань, більшу або рівнішу  3,5. За допомогою координатної прямої 

знаходимо рішення:

х ≤ –6; х ≥ 1.

ВІДПОВІДЬ:  х ≤ –6; х ≥ 1

ПРИКЛАД:

Розв’яжіть нерівність:     

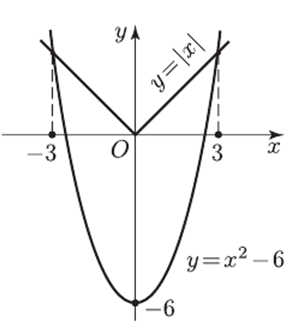
х² – 6 ˃ |x|.

РОЗВ'ЯЗАННЯ:

На малюнку зображені графіки парних функцій

у = х² – 6

у = |x|.

Вирішивши рівняння

х² – 6 = x,

знайдемо його позитивний корінь  х = 3.

Графік функції

у = х² – 6

лежить вище за графік функції

у = |x|

поза відрізком  [–3; 3]. Тому безліч рішень цієї нерівності - сукупність проміжків

х < –3,  и  х ˃ 3.

ВІДПОВІДЬ: 

х < –3,  х ˃ 3

ПРИКЛАД:

Розв’яжіть нерівність:     

|х² – 5x + 2| ˃ 2.

РОЗВ'ЯЗАННЯ:

Ця нерівність рівносильно сукупності нерівностей:

х² – 5x + 2 ˃ 2,

х² – 5x + 2 < –2.

Безліч рішень першої нерівності, рівносильної нерівності

х(х – 5) ˃ 0,

є об'єднанням проміжків

х < 0  и  х ˃ 5.

Безліч рішень другої нерівності, рівносильної нерівності

(х – 1)(х – 4) < 0,

є інтервал

(1; 4)

ВІДПОВІДЬ: 

х < 0,  1 < х < 4,  х ˃ 5

ПРИКЛАД:

Розв’яжіть нерівність:     

|х² + x – 6| ˃ 2 – х.

РОЗВ'ЯЗАННЯ:

Перший спосіб.

Число  х = 2  не є рішенням цієї нерівності, а при  х ˃ 2  нерівність справедлива. Його ліва частина ненегативна при усіх  х ∈ R, а права негативна.

Якщо  х < 2, та початкова нерівність рівносильне сукупності нерівностей:

х² + x – 6 ˃ 2 – х,

х² + x – 6 < –2 + х.

Ці нерівності рівносильні нерівностям:

(х + 4)(х – 2) ˃ 0,

(х + 2)(х – 2) < 0

відповідно.

Вирішивши систему:

отримуємо  х < –4.
Аналогічно з системи

витікає, що

–2 < х < 2.

Так само, безліч рішень цієї нерівності – об'єднання проміжків

х < –4,  –2 < х < 2,  х ˃ 2.

ВІДПОВІДЬ: 

х < –4,  –2 < х < 2,  х ˃ 2

Другий спосіб.

Побудуємо графіки функцій:

у =  |х² + x – 6|,

у = 2 – х.

Ці графіки мають загальну точку  А(2; 0). Дві інші загальні точки отримаємо, знайшовши негативні корені рівнянь 

х² + x – 6 = 2 – х,

6 – х² – x = 2 – х.

Такими коренями є 

х₁ = –2  и  х₂ = –4.

На графіці видно, що графік функції  

у =  |х² + x – 6| 

лежить вище за графік функції  у = 2 – х, при 

х < –4,  –2 < х < 2,  х ˃ 2.

ВІДПОВІДЬ: 

х < –4,  –2 < х < 2,  х ˃ 2

ПРИКЛАД:

Розв’яжіть нерівність:     

|х² – x – 3| < 9.

РОЗВ'ЯЗАННЯ:

Ця нерівність рівносильна системі нерівностей:

яка рівносильна наступній системі нерівностей:

Безліч рішень першої нерівності – інтервал  (–3, 4), друга нерівність є вірною при усіх  х ∈ R.

ВІДПОВІДЬ:  –3 < х < 4

ПРИКЛАД:

Розв’яжіть нерівність:

РОЗВ'ЯЗАННЯ:

Розглянемо два випадки:

1)  х ≤ 0,

2)  х ˃ 0.

Перший випадок.

Якщо  х ≤ 0, то 

|x| = –х  нерівність набере вигляду:

Ця нерівність рівносильна наступної нерівності:

Звідси знаходимо:

–6 < х < –2.

Другий випадок.

Якщо  х ˃ 0, то початкова нерівність (за умови  х ≠ 5) рівносильна нерівності

(х + 6)(х + 2) < 0,

звідки отримуємо:

2 < х < 5, 5 < х < 6

ВІДПОВІДЬ: 

–6 < х < –2, 2 < х < 5, 5 < х < 6

Завдання до уроку 11

• Завдання 1
• Завдання 2
• Завдання 3

Інші уроки:

• Урок 1. Числові нерівності
• Урок 2. Властивості числових нерівностей
• Урок 3. Додавання і добуток числових нерівностей
• Урок 4. Числові проміжки
• Урок 5. Лінійні нерівності
• Урок 6. Системи лінійних нерівностей
• Урок 7. Нелінійні нерівності
• Урок 8. Системи нелінійних нерівностей
• Урок 9. Дробово-раціональні нерівності
• Урок 10. Рішення нерівностей за допомогою графіків
• Урок 12. Ірраціональні нерівності
• Урок 13. Нерівності з двома змінними
• Урок 14. Системи нерівностей з двома змінними
• Урок 15. Наближені обчислення
• Урок 16. Абсолютна і відносна погрішність