Графік відношення, заданої
нерівності з двома змінними, є безліч
точок площини, координати яких є рішеннями цієї нерівності.
у > –0,5х + 4.
Графічне рішення
нерівностей з двома змінними.
Відомо, що пара дійсних
чисел (х; у) однозначно визначає точку координатної
площини. Це дає можливість зображувати рішення нерівності з двома змінними
геометрично, у вигляді деякої безлічі точок координатної площини.
ПРИКЛАД:
Знайти
безліч точок координатної площини, що задовольняють нерівності:
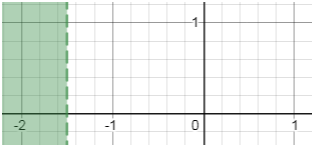
2х + 3 < 0.
РОЗВ'ЯЗАННЯ:
Ах + Ву + С = 0
розділяє площину на дві
напівплощини, в одній з яких виконується нерівність
Ах + Ву + С < 0,
а в іншій – нерівність
Ах + Ву + С ˃ 0.
Щоб вирішити ці
нерівності, досить узяти яку-небудь точку М1(х1; у1),
що
не лежить на прямій
Ах + Ву + С = 0,
і визначити знак числа
Ах1
+ Ву1 + С.
ПРИКЛАД:
Знайти
безліч точок координатної площини, що задовольняють нерівності:
2у – 3х
– 6 < 0.
РОЗВ'ЯЗАННЯ:
Рівняння
2у – 3х
– 6 = 0
є
рівнянням прямої, що проходить через точки
Нехай М1(х1; у1)
– точка, що лежить нижче прямий l
(заштрихованій
на малюнку напівплощині), а М2
– точка з абсцисою х1 і ординатою
у2,
що лежить на прямій l. Тоді
2у2 – 3х1 – 6 = 0, а
2у1 – 3х1 – 6 < 0,
оскільки у1 < у2.
Таким
чином, у будь-якій точці М(х; у),
що лежить нижче прямий l, виконується нерівність
2у1 – 3х1 – 6 < 0.
Аналогічно,
у будь-якій точці М(х; у),
що лежить вище прямий l, виконується
нерівність
2у1 – 3х1 – 6 ˃ 0.
Так само можна вирішити
нерівність загального вигляду:
Ах + Ву + С < 0,
де принаймні одно з
чисел А і В не дорівнює нулю.
Якщо В ˃ 0, то
нерівність
Ах + Ву + С < 0
виконується що в усіх
точках лежать нижче прямої, заданої рівнянням
Ах + Ву + С = 0.
Якщо В < 0, то
нерівність
Ах + Ву + С < 0
справедливо в точках,
що лежать вище за цю пряму.
Якщо В = 0, то
нерівність
Ах + Ву + С < 0
набере вигляду
Ах + С <
0
Ця нерівність
рівносильна нерівності
х < –С/А при А ˃ 0
і нерівності
х ˃
–С/А при А < 0.
ПРИКЛАД:
Знайти
безліч точок координатної площини, що задовольняють нерівності:
3х – 4у
– 12 < 0.
РОЗВ'ЯЗАННЯ:
Нерівність
3х – 4у
– 12 < 0
вірно
в напівплощині, розташованій вище за пряму
так
як при х = у = 0 вираження
3х – 4у
– 12
негативно.
Ця пряма проходить через точки
(4;
0) і (0; –3)
ПРИКЛАД:
Зображувати
на координатній площині безліч рішень нерівності
х
+ у – 1 ˃ 0.
РОЗВ'ЯЗАННЯ:
Перетворимо
цю нерівність до виду
у
˃ –х + 1.
Побудуємо
на координатній площині пряму
у
= –х + 1.
Оскільки
ордината будь-якої точки, що лежить вище за пряму
у
= –х + 1,
Знайти
безліч точок координатної площини, що задовольняють нерівності:
у ˃ –0,5х + 4.
є пряма.Виберемо на цій прямій яку-небудь точку А і проведемо через точку А пряму l, паралельну осі у. Координати точки А задовольняють рівнянню
Вирішити
нерівність:
2х + 5у
˃ 7.
РОЗВ'ЯЗАННЯ:
Можна
підставити будь-яку пару чисел і перевірити, виконалася нерівність або ні. Якщо
нерівність виконалася, то ми вибираємо в якості рішення ту область, якій
належить ця пара чисел, якщо не виконалося, то вибираємо протилежну область.
Виберемо
пару
(1; 2)
Значить, потрібно вибрати область вище за пряму. Область, в якій виконується наша нерівність зазвичай прийнято зображувати штрихуванням або іншим кольором.
ПРИКЛАД:
Зображуйте
в координатній площині безлічі рішень нерівності:
2х + 3у
< 6.
РОЗВ'ЯЗАННЯ:
Накреслимо
графік рівняння
Пара (0;0) є рішенням нерівності
2х + 3у
< 6,
і
належить нижній напівплощині, означає графіком нерівності
2х + 3у
< 6
Зображувати
на координатній площині безліч рішень нерівності
х(х – 2) ≤ у – 3.
РОЗВ'ЯЗАННЯ:
Перетворимо
нерівність до виду
у
≥ х2 – 2х + 3.
Побудуємо
на координатній площині параболу – графік функції
у
= х2 – 2х + 3.
Оскільки
ордината будь-якої точки, параболи, що лежить вище
у
= х2 – 2х + 3,
більше,
ніж ордината точки, що має ту ж абсцису, але що лежить на параболі, і оскільки
нерівність
у
≥ х2 – 2х + 3
нестроге,
то геометричним зображенням рішень заданої нерівності буде безліч точок
площини, що лежать на параболі
у
= х2 – 2х + 3
ПРИКЛАД:
Вирішити
нерівність:
ху < 3.
РОЗВ'ЯЗАННЯ:
Розглянемо
три можливі випадки:
1) х = 0,
то отримуємо вірну нерівність 0 < 3. Що означає, нерівність
виконується для будь-кого у, якщо х = 0.
2) х ˃ 0.
Перейдемо до нерівності у < 3/х.
У правій напівплощині цій нерівності задовольняють безліч усіх точок,
розташованих нижче прямий
у
= 3/х.
3) х < 0.
Перейдемо до нерівності у ˃
3/х.
У лівій напівплощині цій нерівності задовольняють безліч усіх точок,
розташованих вище за пряму
у
= 3/х.
зображений графік нерівності
На
координатній площині зображувати безліч точок, координати яких задовольняють
нерівності:
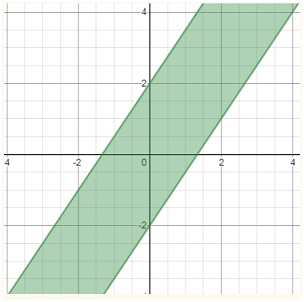
|3х – 2у|
≤ 4.
РОЗВ'ЯЗАННЯ:
Використовуючи
властивість модуля, запишемо цю нерівність у вигляді подвійної нерівності:
–4
≤ 3х
– 2у
≤ 4
і
виразимо з нього у. Отримуємо:
–4
– 3х
≤ –2у
≤ 4 – 3х,
Ці
прямі розбивають точки координатної площини на область, розташовану між ними, і
область, розташовану за ними. Перевірка показує, що цій нерівності
задовольняють точки, розташовані між цими прямими (ці точки заштриховані). Наприклад, для початку координат (контрольна точка х = 0, у = 0) отримуємо, що ця нерівність
|3х – 2у|
≤ 4
виконується
- Урок 1. Числові нерівності
- Урок 2. Властивості числових нерівностей
- Урок 3. Додавання і добуток числових нерівностей
- Урок 4. Числові проміжки
- Урок 5. Лінійні нерівності
- Урок 6. Системи лінійних нерівностей
- Урок 7. Нелінійні нерівності
- Урок 8. Системи нелінійних нерівностей
- Урок 9. Дробово-раціональні нерівності
- Урок 10. Рішення нерівностей за допомогою графіків
- Урок 11. Нерівність з модулем
- Урок 12. Ірраціональні нерівності
- Урок 14. Системи нерівностей з двома змінними
- Урок 15. Наближені обчислення
- Урок 16. Абсолютна і відносна погрішність
















Комментариев нет:
Отправить комментарий