ВИДЕО УРОК
Нерівності виду
де Рn(x); Qm(x) – многочлени, де відповідно n і m, показники степеня, тобто,Рn(x) = anxn
+ an-1xn-1 + … + a1x + a0;
Qm(x) = bmxm
+ bm-1xm-1 + … + b1x + b0;
Рішення раціональних нерівностей виду(замість знаку ˃ може бути і будь-який інший знак нерівності), де Рn(x); Qm(x) – многочлени, ґрунтовано на наступному міркуванні.
Розглянемо вираження:де a < b < c < d.
Якщо x ˃
d, о кожен з
множників
x
– a, x – b, x – c, x – d
позитивний і, отже, на проміжку (d; +∞) маємо
h(x) ˃ 0.
Якщо c
< x < d, то x –
d < 0, а інші множники як і раніше
позитивні. Значить, на інтервалі (c; d) маємо h(x) < 0.
На тих проміжках, де ця крива проходить вище за
координатну пряму, виконується нерівність
h(x) ˃ 0,
на тих же проміжках, де крива проходить нижче прямої, маємо h(x) < 0.
a1, a2, …, an, b1, b2,
…, bk
попарно різні. Зміну знаків функції y
=
f(x) можна також ілюструвати за допомогою кривої
знаків, яку креслять справа наліво, починаючи згори, і проводять через усі
відмічені на координатній прямій точки
a1, a2, …, an, b1, b2,
…, bk.
На цьому заснований метод проміжків, який з успіхом
застосовується для вирішення раціональних нерівностей.
Рn(x) ×Qm(x) ˃ 0 (Рn(x)×Qm(x) <
0).
А × В ˃ 0.
Тому строгу дробову нерівність завжди можна замінити
рівносильною до неї цілою алгебраїчною нерівністю.
(x2 – 3x – 5)(3x2 + 2x – 1) ˃ 0,
Оскільки ці нерівності рівносильні (еквівалентні).
Для того, щоб вирішити нерівність
Рn(x)×Qm(x) ˃ 0,
необхідно розкласти многочлени
Рn(x)
и Рm(x)
а x1, x2, … , xn
– корені рівняння
Рn(x)
= 0.
Безліччю рішень нестрогої нерівності
Рn(x)×Qm(x) ≥
0 (Рn(x)×Qm(x) ≤ 0)
є об'єднанням двох великих кількостей: безліч рішень
строгої нерівності
Рn(x) ×Qm(x) ˃ 0 (Рn(x)×Qm(x) <
0)
і безліч рішень рівняння
Рn(x) ×Qm(x) = 0.
ПРИКЛАД:
х
˃ –1/2, х ˃
2/3,
тобто
х
˃ 2/3.
З
другої системи знаходимо:
х
< –1/2, х
< 2/3,
тобто
х
< –1/2.
У результаті отримали наступні рішення заданої нерівності:
х
< –1/2, х ˃
2/3.
ВІДПОВІДЬ:
х
< –1/2, х ˃
2/3
ПРИКЛАД:
–
якщо чисельник менше або дорівнює нулю, а знаменник більше нуля;
–
якщо
чисельник більше або дорівнює нулю, а знаменник менше нуля;
х
≤ 6, х
˃ 7/2,
тобто
7/2 < х ≤
6.
З
другої системи знаходимо:
х
≥ 6, х
< 7/2,
тобто
система не має рішень.
Значить,
безліч рішень заданої нерівності є проміжок:
(7/2;
6].
ВІДПОВІДЬ: (7/2;
6]
ПРИКЛАД:
Дана
нерівність рівносильна до
(х + 3)(х – 2)(х – 5) < 0.
Корені
многочлена
(х + 3)(х – 2)(х – 5)
дорівнюють:
– 3, 2, 5.
–∞ < х
< –3 і
2 < х < 5.
x2 + 3x + 9
= 0 і
x2 – 2x + 4
= 0
негативні
(D1 = –27 < 0 и D2 = –12 < 0);
отже,
вони рішень не мають.
Відсутність
рішень означає, що квадратні тричлени на множники не розкладаються і на усьому
проміжку зміни х мають постійний знак, співпадаючий зі знаком
старшого члена (у нашому випадку <<+>>).
Помножимо
і розділимо початкову нерівність на позитивні вирази
x2 + 3x + 9
= 0 і
x2 – 2x + 4 =
0.
(х – 3)(х + 2) < 0.
–2 < х ≤ 3.
ВІДПОВІДЬ: (–2;
3]
ПРИКЛАД:
Лінійна
функція х – а
міняє знак під час
переходу через точку а, причому правіше за точку а ця функція позитивна, а лівіше за точку а
– негативна.
Відмітивши
на числовій осі точки
–3, –1, 2, 4,
Під
час переходу через кожну з відмічених точок один і тільки один з цих множників
міняє знак, і тому знак дробу кожного разу міняється. Враховуючи це, розставимо
знаки дробу (дивіться
малюнок). Так, безліч рішень –
об'єднання наступних інтервалів:
(–∞; –3), (–1; 2), (4;
+∞).
ВІДПОВІДЬ:
х
< –3, –1 < х
< 2, х
˃ 4
ПРИКЛАД:
ВІДПОВІДЬ:
–8 ≤ х <
–4, 1
≤ х < 6
ПРИКЛАД:
(х – 3)
і (х + 1),
які
не можуть дорівнювати 0.
Перша
нерівність має рішення
х < –1 и
х
˃ 3.
Вирішуємо
методом інтервалів другу нерівність, його рішення
–4 ≤ х < –1,
3 < х ≤ 4.
ПРИКЛАД:
Квадратний
тричлен
2х2 – 5х – 3
має
корни
х
= –1/2 и х
= 3.
Тому
2х2 – 5х – 3 =
2(х + 1/2)( х – 3).
Квадратний
тричлен
3х2 – 4х + 2
набуває
позитивних значень при усіх х ∈ R, оскільки його дискримінант
D = 16 – 24 < 0,
а
старший коефіцієнт позитивний.
Позначимо
ліву частину нерівності через Р(х). Функція Р(х) не визначена при
х =
7/3 і х = 2
і
міняє знак під час переходу через точки
(х + 1/2)( х – 1)(х – 7/3)( х – 3) ˃ 0.
Застосовуючи
метод інтервалів, знаходимо усі рішення початкової нерівності з урахуванням
того, що числа
–1/2, 1,
и 3
належать
безлічі рішень нерівності, а число 2
не належить цій множині.
ВІДПОВІДЬ:
х
≤ –1/2,
1 ≤ х < 2,
2 < х < 7/3, х ≥
3
ПРИКЛАД:
Перенесемо 1 в ліву частину нерівності з протилежним знаком.
Приведемо до спільного знаменника і розкриємо дужки в чисельнику.Приведемо подібні члени в чисельнику і розкладемо знаменник на множники, користуючись формулою різниці квадратів двох чисел.Помножимо обидві частини нерівності на –1, не забувши поміняти знак нерівності на протилежний.Накреслимо криву знаків для функціїЗ її допомогою знаходимо рішення нерівності:–5 < х
< –1, х ˃ 1.
ВІДПОВІДЬ:
–5 < х
< –1, х ˃ 1
ПРИКЛАД:
y = f(x), де
ілюструємо за допомогою кривої знаків.Значення х, при яких f(x) < 0 (заштриховано), задовольняють наступним нерівностям:
х
< –5,
–√͞͞͞͞͞2 < х
< –5/4,
3/2 < х
< √͞͞͞͞͞3.
Це
рішення початкової нерівності.
ВІДПОВІДЬ:
х
< –5,
–√͞͞͞͞͞2 < х
< –5/4,
3/2 < х
< √͞͞͞͞͞3
Завдання до уроку 9
- Урок 1. Числові нерівності
- Урок 2. Властивості числових нерівностей
- Урок 3. Додавання і добуток числових нерівностей
- Урок 4. Числові проміжки
- Урок 5. Лінійні нерівності
- Урок 6. Системи лінійних нерівностей
- Урок 7. Нелінійні нерівності
- Урок 8. Системи нелінійних нерівностей
- Урок 10. Рішення нерівностей за допомогою графіків
- Урок 11. Нерівність з модулем
- Урок 12. Ірраціональні нерівності
- Урок 13. Нерівності з двома змінними
- Урок 14. Системи нерівностей з двома змінними
- Урок 15. Наближені обчислення
- Урок 16. Абсолютна і відносна погрішність
























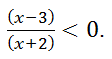




























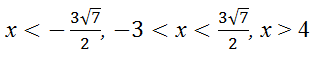





Комментариев нет:
Отправить комментарий