ВИДЕО УРОК
И в природе, и в
технике очень часто встречаются движения, траектории которых представляют собой
не прямые, а кривые линии. Называют такие движения криволинейными.
ПРИМЕР:
По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники, а на Земле – всевозможные средства транспорта, части машин и механизмов, воды рек, воздух атмосферы и т. д.
При криволинейном движении решать задачи механики труднее, потому что оно сложнее прямолинейного. При таком движении уже нельзя сказать, что изменяется только одна координата тела. Если движение происходит на плоскости, то, как это видно из рисунка
при движении изменяются две координаты: х и у. Направление движения, т. е. направление вектора скорости, также всё время изменяется. Изменяется и направление вектора ускорения. Если к этому добавить, что могут изменяться и модули скорости и ускорения, то станет ясно, насколько сложно криволинейное движение.
Так
как для решения задач механики особенно важно уметь вычислить значения скорости
и ускорения, то прежде всего надо выяснить, как изменяются эти величины.
Перемещение и скорость при криволинейном движении.
При прямолинейном движении направление вектора скорости всегда совпадает с направлением перемещения. Что можно сказать о направлении скорости перемещения при криволинейном движении ? Чтобы ответить на этот вопрос, надо воспользоваться тем же приёмом, которым пользовались при изучении мгновенной скорости прямолинейного движения.
На
рисунке
представлена некоторая криволинейная траектория. Допустим, что тело движется по ней из точки А в точку В. При этом пройденный телом путь – это дуга АВ, а его перемещение – это вектор
Конечно, нельзя считать, что скорость тела во время движения направлена вдоль вектора перемещения. Проведём между точками А и В ряд хорд
и представим себе, что движение тела происходит именно по этим хордам. На каждой из них тело движется прямолинейно и вектор скорости
направлен вдоль хорды.
Сделаем
теперь наши прямолинейные участки (хорды) более короткими.представлена некоторая криволинейная траектория. Допустим, что тело движется по ней из точки А в точку В. При этом пройденный телом путь – это дуга АВ, а его перемещение – это вектор
Конечно, нельзя считать, что скорость тела во время движения направлена вдоль вектора перемещения. Проведём между точками А и В ряд хорд
и представим себе, что движение тела происходит именно по этим хордам. На каждой из них тело движется прямолинейно и вектор скорости
направлен вдоль хорды.
По–прежнему на каждом из них вектор скорости направлен вдоль хорды. Но видно, что ломаная линия на рисунке
уже более похожа на плавную кривую. Ясно поэтому, что, продолжая уменьшать длину прямолинейных участков, мы их как бы стянем в точки, и ломаная линия превратится в плавную кривую. Скорость же в каждой точке этой кривой будет направлена по касательной к кривой в этой точке.
Скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
ПРИМЕР:
В том, что скорость при криволинейном движении действительно направлена по касательной, убеждает нас наблюдение за работой точила.
Если прижать к вращающемуся точильному камню концы стального прутка, то раскалённые частицы, отрывающиеся от камня, будут видны в виде искр. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Хорошо видно, что направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной к окружности движутся и брызги от колёс буксирующего автомобиля.
Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различные направления.
Модуль же скорости может быть во всех точках траектории одинаковым
или изменяться от точки к точке, от одного момента времени к другому.
Ускорение при криволинейном движении.
При криволинейном движении точки направление её скорости всё время изменяется, а модуль скорости может как изменяться, так и оставаться постоянным. Но даже если модуль скорости не изменяется, её всё равно нельзя считать постоянной. Ведь скорость – величина векторная. А для векторных величин модуль и направление одинаково важны. Поэтому криволинейное движение всегда движение ускоренное.
Как
изменяется скорость по модулю нам известно. Ведь при равноускоренном
прямолинейном движении изменяется именно модуль скорости. В этом случае вектор
ускорения направлен вдоль вектора скорости или против него, а модуль ускорения
определяется изменением модуля скорости в единицу времени, поэтому в дальнейшем
будет рассматриваться только такое криволинейное движение, при котором модуль
скорости остаётся всё время постоянным, так что ускорение будет связано только
с изменением направления вектора скорости. Как направлено и чему равно это
ускорение ?
И
модуль, и направление ускорения должны, очевидно, зависеть от формы
криволинейной траектории. Но нам не придётся рассматривать каждую из
бесчисленных форм криволинейных траекторий. На рисунке показана сложная
траектория, по которой движется тело.Видно, что отдельные участки криволинейной траектории представляют собой приблизительно дуги окружностей, изображённых тонкими линиями. Например, участок KL или BM – это дуги окружностей малых радиусов, участок EF – это дуга окружности большего радиуса.
Таким
образом, движение по любой криволинейной траектории можно приближённо
представить как движение по дугам некоторых окружностей. Поэтому задача
нахождения ускорения при криволинейном движении сводится к отысканию ускорения
при равномерном движении тела по окружности.
Движение тела, брошенного горизонтально.
Тело, брошенное горизонтально, одновременно участвует в двух движениях: в равномерном по горизонтали (по инерции) и в равноускоренном по вертикали (под действием силы тяжести). Траектория результирующего движения – парабола с вершиной в точке бросания тела. Время движения тела по параболе равно времени свободного падения с той же высоты.
Отсюда
видно, что если тело участвует одновременно в нескольких движениях, то каждое
из них происходит независимо от других. Это положение механики называется принципом независимости движения.
ЗАДАЧА:
Камень брошен в горизонтальном направлении. Через 0,5 сек после начала движения численное значение скорости камня стало в 1,5 раза больше его начальной скорости. Найти начальную скорость камня. Сопротивлением воздуха пренебречь.
РЕШЕНИЕ:
Скорость камня в любой момент времени выражается через её горизонтальную v1 и вертикальную v2 составляющие по формуле
Поскольку
v = 1,5v1, а v2 = gt, то
ОТВЕТ: v1 = 4,4 м/сек
Движение тела, брошенного под углом к горизонту.
Движение тела, брошенного под углом к горизонту, является сложным, как и движение тела, брошенного горизонтально: оно состоит из равномерного прямолинейного движения вдоль линии бросания (по инерции) и равноускоренного движения по вертикали (под действием силы тяжести). Результирующее движение происходит по параболе. Траектория тела, брошенного под углом к горизонту, симметрична относительно высшей точки параболы.
В
действительности сопротивление воздуха уменьшает высоту полёта, дальность
полёта и изменяет форму траектории, делая её нисходящую часть более крутой, чем
восходящую (баллистическая кривая).
ЗАДАЧА:
Тело брошено под углом α = 30° к горизонту со скоростью v0 = 49 м/сек. Определить время полёта, дальность полёта и высоту подъёма тела. Сопротивлением воздуха пренебречь.
РЕШЕНИЕ:
Разложим начальную скорость тела v0 на горизонтальную и вертикальную составляющие:
v1 = v0 cos α
Горизонтальная составляющая является скоростью равномерного движения тела по инерции, и для любого момента времени она имеет одно и то же значение. Вертикальная же составляющая является скоростью равномерного движения, и для любого момента времени равна
v2 = v0 sin α – gt.
В высшей точке траектории вертикальная составляющая скорости равна нулю, т. е. v2 = 0. Тогда время поднятия t' тела на максимальную высоту определится из равенства
0 = v0 sin α – gt',
откуда
Так как время подъёма тела равно времени его падения, то время полёта тела
Дальность полёта
Высота подъёма тела обусловлена лишь вертикальной составляющей скорости:
ОТВЕТ:
s = 212 м, H ≈ 30,6 м.
Задания к уроку 11
Другие уроки:
- Урок 1. Движение материальной точки
- Урок 2. Равномерное прямолинейное движение
- Урок 3. График скорости и пути равномерного прямолинейного движения
- Урок 4. Векторные и скалярные величины
- Урок 5. Действия над векторами и их проекциями
- Урок 6. Неравномерное прямолинейное движение
- Урок 7. Ускорение
- Урок 8. Перемещение при прямолинейном равноускоренном движении
- Урок 9. Средняя скорость при прямолинейном равноускоренном движении. Связь между перемещением и скоростью
- Урок 10. Частные случаи прямолинейного равноускоренного движения
- Урок 12. Движение по окружности
- Урок 13. Вращение твёрдого тела














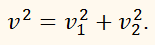






Комментариев нет:
Отправить комментарий