Логарифмическими называют такие уравнения, в которых неизвестные входят
под знак логарифма.
При решении логарифмических уравнений часто приходится логарифмировать и
потенцировать обе две части уравнения. Тоже самое бывает и при решении показательных
уравнений. Указанные операции могут привести к уравнениям, не равносильным данным.
Так, если А и В будут выражениями, которые содержат неизвестные,
то не всегда равносильны такие уравнения:
А
= В
і lg A = lg B,
lg (AВ) = lg С і lg A + lg B = lg С,
lg А/В = lg С і lg
A – lg B = lg С,
lg An = С і n lg A = С.
Для логарифмических уравнений, так же как и для показательных, общего метода
решения нет. Однако среди логарифмических уравнений можно выделить несколько
групп, которые решаются элементарными методами. Приступая до решения уравнений,
необходимо установить область допустимых значений для неизвестного.
Наипростейшими логарифмическими уравнениями называют уравнения вида
lоgа х = b,
где а – отличное от 1 положительное число.
При любом действительном b уравнение имеет единственное
решение
х = аb.
ПРИМЕР:
Решите уравнение:
loga f(x) = b,
где а – отличное от 1 положительное число, а
f(x) – элементарная алгебраическая функция.
Введением неизвестного
t = f(x)
уравнение сводится до наипростейшего логарифмического уравнения
loga t = b.
ПРИМЕР:
Решите уравнение:
log3
(х2 – 7х + 21) = 2.
Область допустимых значений
для х –
вся числовая ось, поэтому
х2 –
7х + 21 > 0
при любом х (дискриминант D
< 0). По определению логарифма
х2 –
7х + 21 = 32,
х1 =
3, х2
= 4.
ПРИМЕР:
Решите уравнение:
logх-1 (х2 – 5х + 2,25) = 2.
Область допустимых значений неизвестного
определяется из условий
х – 1 > 0, х – 1 ≠ 1,
х2 –
5х + 2,25 > 0.
Поэтому, х > 4,5.
Решение данного уравнения сводится
до решения уравнения:
х2 –
5х + 2,25 = (х – 1)2,
–3х = –1,25, х = 5/12.
х = 5/12 не
входить в область допустимых значений.
Уравнение не имеет действительных
корней.
Логарифмическое уравнение вида
loga f(x) = loga φ(x),
где а – отличное от 1 положительное число,
f(x) и φ(x) – элементарные алгебраические функции.
Решение данного уравнения сводится к решению уравнения
f(x) = φ(x),
поэтому для решения данного уравнения достаточно найти все решения уравнения
f(x) = φ(x)
и среди их выбрать те, которые принадлежат к области допустимых значений уравнения
loga f(x)
= loga φ(x),
А если уравнение
f(x) = φ(x)
решений не имеет, то их не имеет и уравнение
loga f(x)
= loga φ(x),
ПРИМЕР:
Решите уравнение:
5lg х = 3lg х/2.
Область допустимых значений х > 0,
lg х5 = lg (х/2)3,
х5 =
(х/2)3.
Решая уравнение, получим:
ПРИМЕР:
Решите уравнение:
lg (2х) = 2lg (4х – 15).
Область допустимых значений неизвестного
для
lg (2х) х > 0,
Для lg (4х –
15) имеем
4х – 15 > 0, или х > 15/4.
Поэтому, область допустимых
значений неизвестного уравнения будет
х > 33/4.
Преобразуем данное уравнение:
lg (2х) = lg (4х – 15)2,
2х = (4х – 15)2,
16х2 – 122х + 225 = 0.
Поэтому,
х1 = 9/2, х2 = 31/8.
Поскольку х2 не принадлежит до области допустимых значений
уравнения а х1 будет решением уравнения, то уравнение имеет единственный
корень:
х = 9/2.
Логарифмическое уравнение вида
loga f1 (x) + loga f2 (x)
+ … + loga fs (x) =
loga φ1
(x) + loga φ2
(x) + … +
loga φm (x),
где а – отличное от 1 положительное число, а fi (x) (i = 1, 2, …, s ) і φj (x) (j = 1, 2, …, m) – алгебраическая функция, при этом некоторые из них могут быть постоянными числами.
Уравнения такого вида сводятся до уравнения вида
f1 (x) f2 (x) … fs
(x) = φ1 (x)
φ2 (x) … φm (x).
ПРИМЕР:
Решите уравнение:
lg (3х – 11) + lg (х – 27) = 3.
Найдём сначала область допустимых значений для х.
3х – 11 > 0,
х > 32/3.
х – 27 > 0,
х > 27.
Общая область допустимых значений
х > 27.
Заменив 3 = lg 1000, уравнение перепишем так:
lg [(3х – 11)(х – 27)] = lg 1000,
откуда
(3х – 11)(х – 27) = 1000,
или
3х2 – 92х
– 703 = 0,
х1 =
37, х2
= –19/3.
Поскольку х2 =
–19/3 не принадлежит к области допустимых значений,
то уравнение имеет единственный корень х
= 37.
ПРИМЕР:
Решите уравнение:
lg (2х) + lg (х + 3) = lg 2 + lg (6х – 2).
Область допустимых значений
для lg (2х): 2х > 0, х > 0,
для lg (х + 3): х +
3 > 0, х > –3,
для lg (6х – 2): 6х
– 2 > 0, х > 1/3.
Уравнение приобретает вид
х(х + 3) = 6х
– 2,
или
х2 –
3х + 2 = 0,
откуда х1 = 2, х2 = 1.
Оба два этих значений принадлежат
к области определения и оба два будут решениями данного уравнения.
Логарифмическое уравнение вида
F[g(x)] = 0,
где g(x) – логарифмическая функция, а F – элементарная алгебраическая функция.
Для решения уравнения вводят переменную
t =
g(x). Тогда данное уравнение сводится до уравнения F(t) = 0.
ПРИМЕР:
Решите уравнение:
(lg х – 5) lg х3 +
18 = 0.
Область допустимых значений х ˃ 0. Так
как
lg х3 = 3lg х,
то данное уравнение равносильно
уравнению
(lg х – 5) 3lg х + 18 = 0.
Обозначим lg х = t, получим
3t (t – 5) + 18 = 0,
t2 –
5t + 6 = 0,
t1 =
2,
t2 = 3.
Решив уравнение
lg х = 2 и lg х = 3,
получим решения данного уравнения:
х1 =
100,
х2 = 1000.
ПРИМЕР:
Решите уравнение:
(lоg2 х)2 – lоg2 х – 2 = 0.
Область допустимых значений х > 0. Обозначим lоg2 х = z, откуда
z2 –
z – 2 = 0, z1
= 2, z2
= –1.
Поэтому,
lоg2 х = 2, х1 = 4,
lоg2 х = –1, х2 = 1/2,
ПРИМЕР:
Решите уравнение:
lоg5 х lоg4
х lоg3 х = 0.
Перепишем уравнение так:
lоg5 х (lоg4
х lоg3 х) = 0.
Тогда число, что стоит в скобках,
по определению логарифма, равно 50, то есть 1:
lоg4 х lоg3
х = 1.
Записывая это уравнение в виде
lоg4 х (lоg3
х) = 1,
получим lоg3 х = 4, откуда
х = 34 = 81.
ПРИМЕР:
Определите х, если:
Определите х, если:
Определите х, если:
Определите х, если:
Определите х, если:
3log2 х = 6,
log2 х = 2, х =
22 = 4.
Задания к уроку 7
Другие уроки:






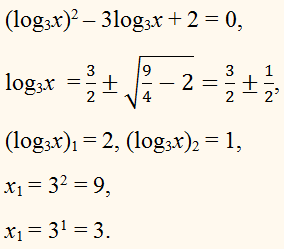
Комментариев нет:
Отправить комментарий