Уроки математики и физики (RU + UA)

▼

пятница, 23 февраля 2018 г.

Урок 15. Об'єм кулі та її частин.

Об'єм кулі.

Уведемо декартові координати, прийнявши центр кулі за початок координат.
Площина  ху  перетинає поверхня кулі радіуса  R  по окружності, що, як відомо, задається рівнянням:

x2 + y2 = R2.

Напівокружність, розташована над віссю  х, задається рівнянням:
Тому об'єм кулі визначається по формулі:
Об'єм кулі  V, радіус якої дорівнює  R, обчислюється за формулою:
Об'єм кульового сегмента.

Кульовим сегментом називається частина кулі, що відтинається від неї площиною.
Формула для об'єму кульового сегмента:
де  R – радіус кулі, а  Н – висота кульового сегмента.
Об'єм кульового сектора.

Кульовим сектором називається тіло, що отримується із кульового сегмента й конуса в такий спосіб:

– якщо кульовий сегмент менше напівкулі, то кульовий сегмент доповнюється конусом, у якого вершина в центрі кулі, а основою є основа сегмента.
– якщо ж сегмент більше напівкулі, то зазначений конус із нього видаляється.
Об'єм кульового сектора одержується додаванням або відніманням об'ємів відповідних сегмента й конуса.
Для об'єму кульового сектора виходить наступна формула:
де  R – радіус кулі, а  Н – кульового сегмента. висота відповідного кульового сегмента.

ЗАДАЧА:

Необхідно переплавити в одну кулю дві чавунні кулі радіусами  

 5 см  і  6 см. 

 Знайти (з точністю до десятих сантиметра) радіус нової кулі.

РОЗВ'ЯЗАННЯ:

Об'єм початкових куль:
Об'єм отриманої кулі:
З іншого боку за відомою формулою:
Маємо:
ВІДПОВІДЬ:  7 см.

ЗАДАЧА:

Визначити, яку частину об'єму кулі становить об'єм сферичного сектора, у якого сферична і конічна поверхні рівновеликі.
РОЗВ'ЯЗАННЯ:

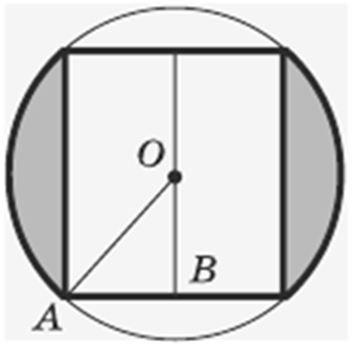
Нехай на рисунку зображено кульовий сектор  АСВО, у якого сферична поверхня рівновелика до конічної.
Якщо позначити  

ОА = R, АD = r  і  
СD = h, то  
2πRh = πrR, 

бо за умовою задачі сферична поверхня кульового сектора дорівнює конічній. В такому випадку  2h = r.
З прямокутного   

∆ ADO (∠ D = 90°), враховуючи, що  
OD = R – h, одержуємо
R2 = (2h)2 + (R – h)2,
звідси  h = 2/5 R.

Об'єм кульового сектора

Vкульов. сект = 2/3 πhR2 = 
4/15 πR3 = 1/5(4/3 πR3),

тобто

Vкульов. сект = 1/5Vкулі.

ВІДПОВІДЬ:  1/5.

ЗАДАЧА:

Площина ділить об'єм кулі у відношенні  7 : 20. В якому відношенні вона ділить поверхню кулі ?

РОЗВ'ЯЗАННЯ:

Нехай площина круга  О1 ділить об'єм кулі у відношенні  7 : 20.
Проведемо діаметр кулі  ВD  перпендикулярно до площини круга  О1  і позначимо  

ВО1 = h, ОВ = R, тоді  
О1D = 2R – h.

За умовою задачі

Vкул. сег. трик. АВС : Vкул. сег. трик. АDС 
= 7 : 20,

 або

πh2(R – 1/3h) : π(2R – h)2[R – 1/3 (2R – h)] 
= 7 : 20.

Звідси після перетворень знаходимо
Замінимо  R = hx  і зазначимо, що оскільки  h < 0, то  x > 1. Тоді
Розкладаючи ліву частину рівняння на множники, одержуємо

(2х – 3)(14х2 + 21х – 9) = 0,

звідки
Оскільки  х > 1, то корені  х2  і  х3  не задовольняють умову задачі, тобто

R = hx1 = 3/2 h,

Тепер знайдемо відношення поверхонь кульового сегмента  

SАВС = S1  і кульового сегментa  
SАDС = S2:
ВІДПОВІДЬ:  1 : 2.

ЗАДАЧА:

У кулі, діаметр якої дорівнює  50 мм, повинен бути просвердлений циліндричний отвір уздовж діаметра кулі. Обчислити об'єм кільцеподібного тіла, що залишився (з точністю до  0,5 см3), якщо діаметр циліндричного отвору дорівнює  30 мм.

РОЗВ’ЯЗАННЯ:

Розглянемо осьовий переріз одержаної конструкції. Побудуємо осьовий переріз кільцеподібного тіла, що вийшов.
Висвердлена частина кулі складається з циліндра і двох сегментів, отже, об'єм, що шукається, дорівнює обсягу кулі без обсягу циліндра і суми обсягів двох сегментів.
Висота циліндра  Н = 2 ∙ ОВ. З прямокутного трикутника  АОВ  знаходимо:
отже, Н = 40 мм.

Висота  h  кожного сегмента дорівнює:

(50 – 40) : 2 = 5 мм.

Позначимо шуканий об'єм буквою  V, тоді:

V = 4/3 πR3 – πr2H – 2πh2(R – 1/3 h).

Після підстановки праву частину рівності замість  R, r, H, h  їх значення, отримаємо:

V = π(4/3∙ 253 – 152∙ 40 – 2∙ 25∙ 52 + 2/3∙ 53).

Після остаточного підрахунку, прийнявши  π = 3,14, знайдемо об'єм:

V ≈ 34 см3.

Завдання до уроку 15
Інші уроки:
на

Комментариев нет:

Отправить комментарий