Уроки математики и физики (RU + UA)

▼

среда, 8 мая 2019 г.

Урок 5. Формула n-го члена арифметичної прогресії

Знаючи перший член арифметичної прогресії  (аn)  і її різниця, можна за допомогою послідовних обчислень знайти будь-який член цієї прогресії.

ПРИКЛАД:

Якщо  a1 = 2,3  и  d = 0,45, то 
a2 = 2,75, a3 = 3,2, a4 = 3,65  и т. д.

Нехай треба знайти десятий член арифметичної прогресії, у якої задані перший член і різниця. Це завдання можна вирішити, знаходячи послідовно усі члени від другого до десятого. Для отримання сотого члена треба виконати ще більшу обчислювальну роботу постараємося знайти коротший спосіб обчислення будь-якого члена арифметичною прогресію
За визначенням арифметичної прогресії.

a2 = a1 + d.
a3 = a2 + d = (a1 + d) + d = a1 + 2d,
a4 = a3 + d = (a1 + 2d) + d = a1 + 3d,
a5 = a4 + d = (a1 + 3d) + d = a1 + 4d,

Легко зміркувати, що

a6 = a1 + 5d,
a10 = a1 + 9d,
a23 = a1 + 22d.

Взагалі,
Наведемо приклади в яких  n-член арифметичної прогресії виражається через перший член, різниця прогресії  d  і номер члена  n.


ПРИКЛАД:

Вимагається знайти  10-ою  і  100-ою  члени арифметичної прогресії  (аn), перший член якої  2,3, а різниця  0,45. Скористаємося формулою:

a10 = 2,3 + 0,45 (10 – 1) = 6,8 – 0,45 = 6,35,
a100 = 2,3 + 0,45 (100 – 1) = 47,3 – 0,45 = 46,85.

ПРИКЛАД:

З'ясуємо, чи є членом арифметичної прогресії

–10;  –5,5;  –1;  3,5; …

число  71.
Перший член цієї арифметичної прогресії рівний  –10, а різниця  4,5. Число  71  є членом цієї прогресії, якщо існує таке натуральне значення змінної  n, при якому значення вираження

–10 + 4,5(n – 1)

рівне  71.
Вирішимо рівняння

–10 + 4,5(n – 1) = 71.

Отримаємо:

4,5(n – 1) = 81,
n – 1 = 18,
n = 19.

Вираження

–10 + 4,5(n – 1)

Набуває значення, рівного  71, при  n = 19, причому  19 – число натуральне. Значить, число  71 – дев'ятнадцятий член цієї прогресії.

ПРИКЛАД:

Між числами  2,5  і  4  вставити два таких числа, щоб вони разом з даними утворювали арифметичну прогресію.
Маємо прогресію  (аn):

2,5;  a2;  a3;  4.

Використавши формулу

an = a1 + d(n – 1)

й урахувавши що

a1 = 2,5,  a4 = 4,

Складемо та розв’яжемо рівняння:

2,5 + 3d = 4,
d = 1,5,  d  = 0,5.

Тоді

а2 = 2,5 + 0,5 = 3,
а3 = 3 + 0,5 = 3,5.

ВІДПОВІДЬ:  3,  3,5

ПРИКЛАД:

Знайдіть перший додатний член арифметичної прогресії:

–10,2;  –9,6;  –9; … .

РОЗВ’ЯЗАННЯ:

а1 = –10,2, a2 = –9,6. Отже,
d = a2 – a1 = –9,6 – (–10,2)  = 0,6.
an = a1 + d(n – 1).

Якщо  an > 0, то  

–10,2 + 0,6(n – 1) > 0,
n – 1 > 17, n > 18.

Отже, перший додатний член  a19.

a19 = –10,2 + 0,6(19 – 1) = 0,6.

ВІДПОВІДЬ:  0,6.

ПРИКЛАД:

Знайдіть перший від’ємний член арифметичної прогресії:

10,5;  9,8;  9,1; … .

РОЗВ’ЯЗАННЯ:

а1 = 10,5, a2 = 9,8. Отже,
d = a2 – a1 = 9,8 – 10,5  = –0,7.
an = a1 + d(n – 1).

Якщо  an < 0, то  

10,5 – 0,7(n – 1) < 0,
0,7(n – 1) > 10,5,
n – 1 > 15, n > 16.

Отже, перший від’ємний член  a17.

a17 = 10,5 – 0,7(17 – 1) = –0,7.

ВІДПОВІДЬ:  –0,7.

ПРИКЛАД:

Розглянемо арифметичну прогресію  (аn), задану умовами

a1 = 6,  d = 4.

Знайдемо  n-й член цієї арифметичної прогресії:

an = 6 + 4(n – 1), т. е.
an = 4n + 2.

Ми отримали формулу, права частина якої – двочлен  4n + 2, що містить змінну  n (n ∈ N)    в першому ступені. Значить, арифметична прогресія  (аn)  є лінійною функцією, заданою на безлічі  N  натуральних чисел формулою

y = 4x + 2.

Графік цієї арифметичної прогресії є безліччю точок з натуральними абсцисами, що належать прямій

y = 4x + 2.

Це, наприклад, точки

(1; 6), (2; 10), (3; 14),

 и др.
Арифметична прогресія є лінійною функцією, заданою на безлічі натуральних чисел.

Для того, щоб довести це, представимо формулу  n- го члена арифметичної прогресії

an = a1 + d(n – 1)

в виді

an = dn + (a1 – d).

Ми отримали формулу виду

y = kx + b,

де  k = d  и  b = a1 – d  – деякі числа,
x = n  і  y = an – змінні, а такою формулою, як відомо, задається лінійна функція.

 Завдання до уроку 5
Інші уроки:
на

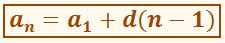
Комментариев нет:

Отправить комментарий