ВІДЕО УРОК
Для введення поняття
координат вектора слід розглянути можливість розкладання вектора по осях
координат. Кожен вектор задається парою чисел – проекціями цього вектора на осі
координат. При такому підході дії над векторами можна звести до дій з парами
чисел.
При цьому береться знак << плюс >>, якщо напрямок векторазбігається з напрямком осі Ох, і знак << мінус >>, якщо ці напрямки протилежні.
Якщотобто А1 = В1, то ах = 0.
Перш ніж ввести поняття
координат вектора, розглянемо наступний приклад.
ПРИКЛАД:
Нехай– деякий вектор, а ах і ау – його проекції на осі координат. Тоді векторєдиний образ представляється у виглядіОтримана формула застосовується для розкладання векторапо векторамПару чисел ах і ау називають координатами векторав даній системі координат.
Будь-вектор є вільним, тому при необхідності можна відкласти його від будь-якої іншої точки площині. Для векторів можна взагалі не будувати осі, прямокутну систему координат, потрібен лише базис, в даному випадку ортонормованій базис площини.ПРИКЛАД:
А(2; 1), В(–2; 3),а сенс координат абсолютно різний, і треба добре розуміти цю різницю.
Векторвиходить з колінеарну йому одиничного векторамноженням наПри цьому, якщосонаправлен зЯкщо жпротилежно спрямованийОтже, має місце рівністьПроекція точки – точка, проекція відрізка – відрізок (або точка), а проекція вектора – число.
Обов'язково потрібно
розуміти різницю між координатами точок і координатами векторів.
Координати
точок – це звичайні координати в прямокутній
системі координат. Кожна точка має суворим місцем на площині, і переміщати їх
куди-небудь не можна.
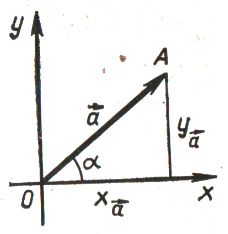
Розглянемо малюнок.Якщо точка А не лежить на координатних осях, то трикутник ОАА1 прямокутний..
ТодіПо теоремі Піфагора.
Так як А1А = ОА2, то отримаємо, що
Координати
рівних векторів відповідно рівні.
Вектори, які мають відповідно рівні координати, рівні.
Координати вектора пов'язані з координатами точки за
таким правилом:
Щоб знайти координати вектора, потрібно від координат кінця
вектора відняти координати початку вектора.
Зокрема, якщо вектор відкладений від початку
координат, то координати вектора дорівнюють координатам його кінця.
Проекція вектора на
заданий напрямок.
Число
ab
= a cos α
Проекція дорівнює нулю, якщо напрями векторіввзаємно перпендикулярні.
Проекції рівних векторів рівні.
Точку А називатимемо кінцем вектора
Координатами вектора називаються координати його кінця,
які позначатимемо
Координати нульового вектора
дорівнюють
Якщо вектор
ненульовий, то він має певний напрям. Напрям вектора
– це не що інше, як напрям, заданий променем ОА. Цей промінь можна дістати з променя Ох (додатного променя осі абсцис) внаслідок повороту Rα.
Якщо обмежити кут α умовами
–180⁰ < α ≤ 180⁰,
то кут α визначатиметься вектором
однозначно. Кажуть, що вектор
утворює кут α з додатним напрямом осі абсцис. Ненульовий вектор цілком визначається завданням його довжини
і кута α, що його утворює вектор з додатним напрямом осі абсцис. Вектор одиничної довжини називається одиничним вектором. Кінець одиничного вектора лежить на одиничному колі. Тому одиничний вектор, що утворює кут α з віссю абсцис, записують у вигляді
Його координати дорівнюють
Візьмемо одиничний вектор
того самого напряму, що й вектор
Відношення
будуть рівними між собою при довільному куті α. Рівність абсолютних величин цих відношень випливає з подібності трикутника OAN і OEM.
Знаки ординат
однакові. Але
тому звідки Аналогічно дістанемо: Рівність абсолютних величин цих відношень випливає з подібності трикутників OAN і OEM. Знаки абсцис однакові. Отже, Звідси Таким чином, вектор який утворює кут α з додатним напрямом осі абсцис, має координати Координати вектора на площині.
що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А. якщо початком вектора є точка А(хА; уА), а кінцем – точка В(хВ; уВ), то
Записують вектор
вказуючи його координати так:
Наприклад:
ПРИКЛАД:
За умовою
Дано точки
А(–2; 3), B(4; –1), C(x; –2), D(0; y).
Знайдіть х і у. Якщо
РОЗВ'ЯЗАННЯ
:тобто АВ = (6; –4).
тобто CD = (–x; y + 2).
Оскільки
то –х = 6 і у + 2 = –4.
Звідки х = –6; у = –6.
Визначення
коллинеарности векторів за допомогою координат вектора.
Якщо вектори колінеарні, то їх відповідні координати
пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні,
то ці вектори колінеарні.
Протилежні вектори мають протилежні
відповідні координати.
Якщо відповідні координати двох векторів протилежні, то вектори
протилежні.
РОЗВ'ЯЗАННЯ:
































































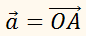








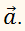









































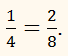




Комментариев нет:
Отправить комментарий