ВІДЕО УРОК
Система координат в
просторі.
Виберемо початок координат. Проведемо три взаємно перпендикулярні осі
Х, Y і Z.
Задамо зручний масштаб.
Вийшла система координат в тривимірному просторі. Тепер кожна його точка характеризується трьома числами – координатами по Х, Y і Z.
ПРИКЛАД:
Запис
М(–1; 3; 2)
означає що координата точки М по Х (абсциса) рівна –1, координата по Y (ордината) дорівнює 3, а координата по Z (апліката) рівна 2.
Вектори в просторі визначаються так само як і на площині. Це спрямовані відрізки, що мають початок і кінець. Тільки у просторі вектор задається трьома координатами x, y і z:
Визначення координат вектору.
Як знайти координати вектору ? Як і на площині – з координати кінця віднімаємо координату початку.
У разі просторового завдання вектор АВ заданий координатами точок
А(XA; YA; ZA) і
B(XB; YB; ZB)
можна знайти скориставшись наступною формулою:
ПРИКЛАД:
Дано точки
F(–2; –1; 0) і
E(0; –1;
–2).
Дано точки
A1(10; 5;
–4),
A2(–8; 6;
3),
A3(1; 1;
–1),
A4(0; 0;
1).
Нехай точка М – середина відрізку АВ. Її координати знаходяться по формулі:
Довжина (модуль) вектору в просторі. Довжина вектору
у просторі – ця відстань, між точками А і В. Якщо вектор заданий своїми координатами:
те його довжина знаходиться по формулі:
де
– модуль вектора,
а1, a2 a3 – його координати.
Одиничним називається вектор
Нульовим називається вектор
у якого початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, а його модуль дорівнює нулю.
Довжина вектору, заданого координатами, дорівнює кореню квадратному з суми квадратів його координат.
ПРИКЛАД:
Дано точки
А(2;
3; –1),
В(–5;
3; 0).
Знайти довжину (модуль) відрізка АВ.
РОЗВ'ЯЗАННЯ:
Дано точки
А(0;
2; 5),
В(–4;
7; 15).
Знайдемо векторОбчислимо довжину вектора.ВІДПОВІДЬ:ПРИКЛАД:
Знайти довжину вектору:
РОЗВ'ЯЗАННЯ:
Для векторурозташованого в просторі, розкладання по ортам координатних осей має вигляд:ПРИКЛАД:
РОЗВ'ЯЗАННЯ:
Використовуючи формулу, отримуємо:
ВІДПОВІДЬ: √͞͞͞͞͞17
ПРИКЛАД:
Знайдіть координати і довжину векторів
якщо
А(2; –3; –1),
В(–4; –8; 5),
С(3; 1; –2)
РОЗВ'ЯЗАННЯ:
ВІДПОВІДЬ:
Рівність векторів у просторі.
ВІДПОВІДЬ: √͞͞͞͞͞17
ПРИКЛАД:
Знайдіть координати і довжину векторів
якщо
А(2; –3; –1),
В(–4; –8; 5),
С(3; 1; –2)
РОЗВ'ЯЗАННЯ:
ВІДПОВІДЬ:
Рівність векторів у просторі.
Якщо
то
Якщо
то
то
Якщо
то
ПРИКЛАД:
Протилежні
вектори у просторі.
ПРИКЛАД:
Які з векторівколінеарні ?
Вектораколінеарні так якВекторане колінеарні так якВекторане колінеарні так якПРИКЛАД:
Знайдіть значення m і n, при яких вектори
колінеарні.
РОЗВ'ЯЗАННЯ:
У колінеарних векторів координати пропорційні, звідси:
Маємо два рівняння:
ВІДПОВІДЬ:
m = 1, n = –10.
Векторине компланарні, так як точки А, В, D і О не лежать в одній площині.
Система ортів (чи базисна система векторів) – це система одиничних векторів осей координат.
Орт координатної осі 0x позначається через
осі 0y – через
осі 0z – через
Нехай в просторі введена прямокутна система координат з одиничними векторамикоординатних осей Ох, Оу, Оz. Тоді векторєдиним образом представляється у виглядіЧисла
РОЗВ'ЯЗАННЯ:
Вектораколінеарні так якВекторане колінеарні так якВекторане колінеарні так якПРИКЛАД:
Знайдіть значення m і n, при яких вектори
колінеарні.
РОЗВ'ЯЗАННЯ:
У колінеарних векторів координати пропорційні, звідси:
Маємо два рівняння:
ВІДПОВІДЬ:
m = 1, n = –10.
Крім поняття коллинеарности векторів, вводиться поняття
компланарности векторів.
Три вектора називають компланарними, якщо зображують їх
спрямовані відрізки лежать в паралельних площинах або в одній площині.
ПРИКЛАД:
Векторине компланарні, так як точки А, В, D і О не лежать в одній площині.
Розкладання вектору по
ортам координатних осей.
Система ортів (чи базисна система векторів) – це система одиничних векторів осей координат.
Орт координатної осі 0x позначається через
осі 0y – через
осі 0z – через
Нехай в просторі введена прямокутна система координат з одиничними векторамикоординатних осей Ох, Оу, Оz. Тоді векторєдиним образом представляється у виглядіЧисла
ax, ay, az
Для векторурозташованого в просторі, розкладання по ортам координатних осей має вигляд:ПРИКЛАД:
Знаючи розкладанняпо базисній системі
векторів:записати
координати цього вектору в просторі.
РОЗВ'ЯЗАННЯ:
Вектор
заданий своїми координатами:
Записати розкладання цього вектору ортам осей координат.
РОЗВ'ЯЗАННЯ:
Координати вектору – це коефіцієнти при ортах координатних осей в розкладанні вектору по базисній системі, тому шукане розкладання:
заданий своїми координатами:
Записати розкладання цього вектору ортам осей координат.
РОЗВ'ЯЗАННЯ:
Координати вектору – це коефіцієнти при ортах координатних осей в розкладанні вектору по базисній системі, тому шукане розкладання:
ВІДПОВІДЬ:
Завдання до уроку 5




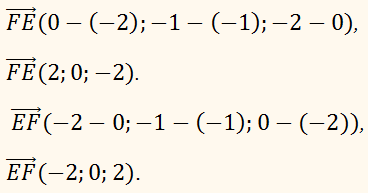

















































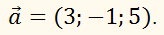

Комментариев нет:
Отправить комментарий