Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
КООРДИНАТИ ВЕКОРА
або
ВІДЕО УРОК
б) 5;
в) √͞͞͞͞͞17;
г) √͞͞͞͞͞15.
2. Дано точки
А(3; 1) і B(–1; 2).
Знайдіть координати вектора
а) (4; –1);
б) (–4; –1);
в) (4; 1);
г) (–4; 1).
3. Знайдіть модуль вектора
а) –2√͞͞͞͞͞5;
б) √͞͞͞͞͞5;
в) 2√͞͞͞͞͞5;
г) –√͞͞͞͞͞5.
4. Укажіть координати вектора
протилежного вектору
а) (–7; –5);
б) (5; –7);
в) (7; 5);
г) (7; –5).
5. Знайдіть модуль вектора
якщо
A(3; –1), B(3; –4).
а) √͞͞͞͞͞61;
б) 3;
в) √͞͞͞͞͞5;
г) √͞͞͞͞͞11.
6. Знайдіть координати вектора
якщо
A(–3; 2), B(–1; –2).
а) (–4; 0);
б) (–2; 4);
в) (2; –4);
г) (4; 0).
7. При якому значенні у вектори
колінеарні ?
а) –15;
б) 15;
в) –2,4;
г) 2,4.
б) 5;
в) √͞͞͞͞͞13;
г) √͞͞͞͞͞5.
9. Дано точки
М(4; –2) і К(2; 1).
Знайдіть координати вектора
а) (2; –3);
б) (–2; 3);
в) (2; 3);
г) (–2; –3).
10. Знайдіть довжину вектора
а) 14;
б) 2;
в) 10;
г) 50.
11. Дано точки
А(–1; 2) і B(3; 1).
Знайдіть координати вектора
а) (4; –1);
б) (–4; –1);
в) (4; 1);
г) (–4; 1).
12. Обчисліть модуль вектора
а) 6;
б) 0;
в) 2√͞͞͞͞͞17;
г) 2√͞͞͞͞͞15.Завдання до уроку 2











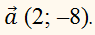
Комментариев нет:
Отправить комментарий