Уроки математики и физики (RU + UA)

▼

понедельник, 16 февраля 2015 г.

Урок 7. Площадь параллелограмма

ВИДЕОУРОК

Основание параллелограмма  а – одна из сторон параллелограмма. Высота параллелограмма  h – перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание.

Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота  ВЕ, проведённая между длинными сторонами, короче высоты  ВF, проведённой между короткими сторонами.

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин  В  и  С  к стороне  АD. Прямоугольные треугольники  АВЕ  и  DСF  равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояния между параллельными прямыми).

Параллелограмм  ABCD  и прямоугольник  EBCF – равновеликие, так как состоят из равных фигур:

SABCD = SABE + SEBCD,

SEBCF = SDCF + SEBCD.

Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:

SEBCF = BE∙ BC,

SABCD = BE∙ BC = BE∙ AD.

Если обозначить сторону через  а, высоту – через  h, то:
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.

ПРИМЕР:

ABCD – параллелограмм.
ВК ⊥ А D,  
ВК = 4 см, 
АD = 6 см,  
S = ВК × АD = 
= 4× 6 = 24 см2.

Площадь параллелограмма равна произведению сторон на синус угла между ними.
Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.
ЗАДАЧА:

Дан параллелограмм  АВСD.

 Найдите площадь параллелограмма, если:

ВС = 10, АК = 5.

АК – перпендикуляр, опущенный из вершины  А  на прямую  ВС.

РЕШЕНИЕ:

ВС – основание, АК – перпендикуляр, проведённый к этому основанию, тогда:

Sпарал. = 10∙ 5 = 50.

ЗАДАЧА:

Дан параллелограмм  АВСD.
Найдите площадь параллелограмма, если:

СD = 6, DL = 10  

(DL ⊥ AB).

РЕШЕНИЕ:

CD – основание, 

DL – высота, тогда:

Sпарал. = 6 ∙ 10 = 60.

ЗАДАЧА:

Площадь параллелограмма равна  32, а две его стороны равны  8  и  16. Найдите его высоты.

РЕШЕНИЕ:

Начертим чертёж.
Для решения этой задачи надо из формулы площади параллелограмма, найти обе высоты.

S = ah.

h1 = 32 : 8 = 4,

h2 = 32 : 16 = 2.

ЗАДАЧА:

Найдите площадь параллелограмма, изображённого на рисунке.
РЕШЕНИЕ:

S = ah.

h = 5 – высота,

а = 12 + 3 = 15 – сторона, к которой проведена высота.

S = 15 ∙ 5 = 75.

ЗАДАЧА:

АВСD – параллелограмм.
Найдите площадь параллелограмма, если

АВ = 6, АD = 7, 

∠ А = 30°.

РЕШЕНИЕ:

Проведём  ВН ⊥ АD, ВН – высота.

Найдём  ВН  из прямоугольного треугольника  АВН. Катет, лежащий против угла  30°, равен половине гипотенузы. Значит,

ВН = 1/2 АВ = 1/2∙ 6 = 3.

Высоту нашли, основание известно, значит, площадь параллелограмма равна:

S = АD∙ ВН = 7∙ 3 = 21.

ОТВЕТ:  21

ЗАДАЧА:

В параллелограмме  АВСD:

АD = а, АВ = b,

ВН = h – высота.
Найдите другую высоту.

РЕШЕНИЕ:

Высота входит в формулу площади параллелограмма. Посчитаем площадь двумя способами: через одну высоту и через другую высоту.
ОТВЕТ:
ЗАДАЧА:

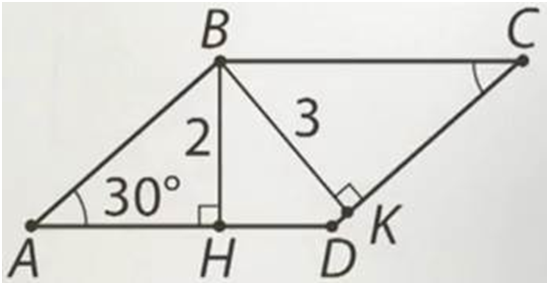
Острый угол параллелограмма равен  30°, а высоты, проведённые из вершины тупого угла, равны  2 см  и  3 см. Найдите площадь параллелограмма.

РЕШЕНИЕ:

Есть параллелограмм  АВСD. Проведём из вершины  В  высоты:  ВН  и  ВК  к прямой  АD  и  DС  соответственно.
Найдём основание параллелограмма. Для этого рассмотрим треугольник  АВН. Он прямоугольный, с углом  30°, катет, лежащий против этого угла, равен  2. Значит, гипотенуза равна:

АВ = 2 ∙ 2 = 4.

Теперь мы имеем основание  АВ  и высоту  ВК, которая проведена к этому основанию. Площадь параллелограмма будет равна:

S = АВ∙ ВК = 4 ∙ 3 = 12.

ОТВЕТ:  12 см2

ЗАДАЧА:

В параллелограмме  АВСD  из точки  А  проведена биссектриса  АL  и перпендикуляр  АН  к прямой  СD.

ВL = 3 м, АН = 4 м.

Найдите площадь параллелограмма.

РЕШЕНИЕ:

Начертим чертёж.
АН – высота, которая проведена из вершины  А  к прямой  СD. Чтобы найти площадь надо узнать длину стороны  СD.

АL – биссектриса, значит, ∠ 1 = ∠ 2, но прямые  АD  и  ВС  параллельны, АL – секущая. Значит, ∠ 2 = ∠ 3  как накрест лежащие углы. Тогда в треугольнике  АВL  ∠ 1 = ∠ 3, то есть это равнобедренный треугольник.

АВ = ВL = 3. Значит,

СD = АВ = 3.

Тогда площадь параллелограмма равна:

S = СD ∙ АН = 4∙ 3 = 12.

ОТВЕТ:  12 см2

ЗАДАЧА:

Высоты параллелограмма равны  5 см  и  4 см, а периметр равен  43 см. Найдите площадь параллелограмма.

РЕШЕНИЕ:

Начертим чертёж.
Площадь параллелограмма равна произведению стороны на высоту, опущенную на эту сторону. Обозначим стороны параллелограмма как  а  и  b. Следовательно, площадь и периметр будут соответственно равны:

S = 4a, S = 5b,

P = 2a + 2b.

Откуда:

4a = 5b,

a = 5/4b.

Поскольку периметр параллелограмма равен  42 см, то

2(5/4b) + 2b = 42

b = 91/3.

Откуда

a = 112/3.

Теперь находим площадь параллелограмма:

S = 4∙ 112/3 = 5∙ 91/3 = 462/3.

ОТВЕТ:  462/3 см2

ЗАДАЧА:

Площадь параллелограмма  АВСD  равна  132. Точка  Е – середина стороны  АВ. Найдите площадь треугольника  СВЕ.

РЕШЕНИЕ:

Для решения этой задачи знание формул не требуtтся Необходимо провести прямую через точку  Е  параллельно стороне  ВС  и  АD.
Так как  E – середина  АВ, то  ЕN  делит параллелограмм на два равных параллелограмма  АЕND  и  ЕВСN. Проведя во втором параллелограмме диагональ, получится четыре равных по площади треугольника.
SEBC = 132 : 4 = 33.

Задания к уроку 7
Другие уроки:
на

Комментариев нет:

Отправить комментарий