где а и b – основания, h – высота трапеции.
ЗАДАЧА:
Основания равнобедренной трапеции равны 15
см и
33 см, а диагональ делит её острый угол пополам. Найдите
площадь трапеции.
РЕШЕНИЕ:
АD = 33 см, ВС = 15 см,
АЕ =
(33 – 15) : 2 = 9 (см).
∠ DАС = ∠ САВ. АD
∥ ВС
і
АС
– секущая,
поэтому ∠ DАС = ∠ АСВ.
Кроме того, ∠ DАС = ∠ САВ по условию.
Поэтому ∠ САВ = ∠ АСВ и треугольник
АВС – равнобедренный. Отже,
АВ = ВС = 15 см.
Sтр. = 1/2
(АD + ВС) ∙
ВЕ =
=
1/2
(33
+ 15) ∙ 12 = 288 (см2).
ОТВЕТ: 288
см2
ЗАДАЧА:
Основания равнобедренной трапеции равны 3
см и
13 см, а диагональ делит её тупой угол пополам. Найдите
площадь трапеции.
РЕШЕНИЕ:
ВК – её высота,
ВD – биссектриса угла В, а значит.
∠1 = ∠2, ∠2 = ∠3,
АD
∥ ВС і ВD – секущая. Поэтому,
∠1 = ∠3 і АВ = АD = 13 см.
АК = (АD – ВС) : 2 = (13 – 3) : 2 = 5 (см).
ЗАДАЧА:
В равнобедренную трапецию вписана окружность. Боковая
сторона точкою касания делится на отрезки длиною 16
см и
9 см. Найдите площадь трапеции.
РЕШЕНИЕ:
СК = 9 см, КD = 16 см,
СР = СК = 9 см
как касательные до окружности,
проведенные из одной точки. Аналогично
ЕD = КD = 16 см.
Проведём
СМ ⊥ АD,
ЕМ = РС = 9 см,
тогда
МD = ЕD – ЕМ =
= 16 – 9 = 7 см.
ВС = 2РС = 2 ∙ 9 = 18 (см).
- Урок 1. Единицы измерения площади
- Урок 2. Площадь прямоугольника
- Урок 3. Площадь квадрата
- Урок 4. Площадь треугольника
- Урок 5. Площадь прямоугольного треугольника
- Урок 6. Площадь равнобедренного треугольника
- Урок 7. Площадь параллелограмма
- Урок 8. Площадь ромба
- Урок 9. Площадь трапеции
- Урок 11. Площадь прямругольной трапеции
- Урок 12. Площадь круга и его частей
- Урок 13. Подобие разносторонних треугольников
- Урок 14. Подобие равнобедренных треугольников
- Урок 15. Подобие прямоугольных треугольников
- Урок 16. Площадь многоугольника








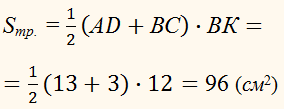



Комментариев нет:
Отправить комментарий