Урок 3. Площадь квадрата

понедельник, 23 февраля 2015 г.

Урок 3. Площадь квадрата

ВИДЕОУРОК
Прямоугольник, у которого длина и ширина равны между собой, называется квадратом.

Площадь квадрата равна произведению его сторон или квадрату его стороны.

Формулы для вычисления площади квадрата.

a – сторона квадрата;

d – диагональ;

Р – периметр;

S – площадь;

R – радиус описанной окружности;

r – радиус вписанной окружности;

l – отрезок изображенный на рисунку (часто применяется в сложных примерах).

ЗАДАЧА:

Во сколько раз изменится площадь квадрата, если его сторону увеличить в 5 раз ?

РЕШЕНИЕ:

Из формулы
видно, что если сторона квадрата увеличится в 5 раз, то его площадь изменится в 25 раз.

S = (5a)² = 25a².

ЗАДАЧА:

Во сколько раз увеличится площадь квадрата, если его диагональ увеличится в 2 раза ?

РЕШЕНИЕ:

Из формулы
видно, что если диагональ квадрата увеличится в 2 раза, то его площадь увеличится в 4 раза.
ЗАДАЧА:

Найдите площадь квадрата ABCD, если АС = 10.

РЕШЕНИЕ:

Начертим чертёж.

АD = СD как стороны квадрата.

По теореме Пифагора находим:

АС² = АD² + СD² = 2∙ АD²,

тогда

2∙ АD²= 100, АD² = 50,

то есть площадь квадрата равна 50.

ЗАДАЧА:

Найти сторону квадрата, равновеликого прямоугольнику со сторонами 9 и 4.

РЕШЕНИЕ:

У равновеликих фигур площади одинаковые, значит площадь прямоугольника

9 ∙ 4 = 36

равна площади квадрата.

Тогда сторона квадрата будет равна:

а = √͞͞͞͞͞36 = 6.

ЗАДАЧА:

Стороны квадрата ABCD разделены точками M, N, K, P в отношении 1 : 2 каждая. Найти отношение площадей квадрата и четырёхугольника.
РЕШЕНИЕ:

Рассмотрим треугольник АМР. Он прямоугольный. Обозначим сторону АМ = х, тогда сторона АР = 2х. Согласно теореме Пифагора сторона
Четырёхугольник MNKP – квадрат со стороною АМ = √͞͞͞͞͞5 х, значит, площадь этого квадрата равна 5х².

Площадь квадрата ABCD будет равна

(х + 2х)² = 9х².

Тогда отношение площадей этих квадратов будет равно:

9х² : 5х² = 9 : 5 = 1,8.

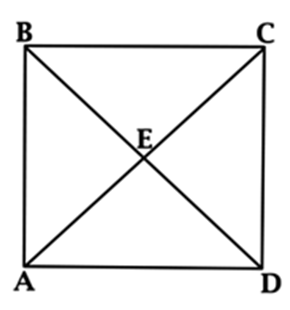
ЗАДАЧА:

В квадрате ABCD расстояние от точки пересечения диагоналей до одной из его сторон равно 5. Найдите площадь этого квадрата.

РЕШЕНИЕ:

Начертим чертёж.

Пусть Е – точка пересечения диагоналей квадрата ABCD. В квадрате диагонали равны, пересекаются и точкой пересечения делятся пополам, тогда

АЕ = ЕD и ∠ DАЕ = ∠ ЕDА.

Так как квадрат является и ромбом, то в квадрате диагонали делят углы пополам, тогда

∠ DАЕ = 0,5 ∙ 90° = 45°, тогда

∠ АED = 180° – 45° – 45° = 90°.

В треугольнике АDЕ опустим из Е высоту ЕF на АD (длина ЕF и есть расстояние от точки Е до стороны). Так как АЕ = ЕD, то ЕF является и медианой, но в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда

ЕF = 0,5∙ АD.

Аналогично остальные расстояния от Е до сторон квадрата равны половине стороны квадрата, тогда АD = 10, следовательно, площадь квадрата ABCD равна 100.

ЗАДАЧА:

Найдите площадь квадрата, если его сторона равна 3 см 6 мм

РЕШЕНИЕ:

Запишем сторону квадрата в миллиметрах. Получим 36 мм. Теперь найдём его площадь в квадратных миллиметрах:

S = 36² = 36 ∙ 36 = 1296 (мм)².

ЗАДАЧА;

Периметр квадрата равен 24 см. Найдите площадь квадрата.

РЕШЕНИЕ:

Периметр равен 4 × а,

где а – это сторона квадрата.

4 × а = 24,

а = 24 : 4 = 6.

= а × а = 6 × 6 = 36 см².

Или по формуле:

ОТВЕТ: 36 см²

ПРИМЕР:

У квадрата сторона 2 см, а у прямоугольника длина 9 см, а ширина 6 см. Какова площадь красной зоны ?

РЕШЕНИЕ:

Площадь квадрата равна 4 см². Он разбит на 4 равных квадрата. Площадь меньшего квадрата равна 1 см², а площадь прямоугольника равна 54 см², поэтому площадь красной зоны равна:

54 – 1 = 53 (см²).

ОТВЕТ: 53 см²

ЗАДАЧА:

На сколько квадратных сантиметров площадь квадрата со стороной 12 см больше площади прямоугольника со сторонами 9 см и 1 см ?

На скільки квадратних сантиметрів площа квадрата зі стороною 12 см більша за площу прямокутника зі сторонами 9 см і 1 см ?

РЕШЕНИЕ:

Площадь квадрата равна:

12 ∙ 12 = 144 (см²).

Площадь прямоугольника равна:

9 ∙ 1 = 9 (см²).

Тогда разность площадей будет равна:

144 – 9 = 135 (см²).

ОТВЕТ:

Площадь квадрата больше площади прямоугольника на 135 (см²).

Задания к уроку 3

Другие уроки:

Уроки математики и физики для школьников и родителей

понедельник, 23 февраля 2015 г.