Уроки математики и физики (RU + UA)

▼

понедельник, 16 января 2017 г.

Урок 11. Площадь прямоугольной трапеции

ВИДЕОУРОК
Для измерения площади прямоугольной трапеции можно воспользоваться формулой для измерения произвольной трапеции. Только необходимо учитывать, что высотой будет сторона, перпендикулярная основаниям.

 Площадь прямоугольной трапеции равна произведению полусуммы её оснований на высоту.
или произведению средней линии на высоту:
где
средняя линия.

ЗАДАЧА:

Основания прямоугольной трапеции равны  24 см  и  16 см, а диагональ – биссектриса её острого угла. Найдите площадь трапеции.

РЕШЕНИЕ:

Пусть АВСD (АD ∥ ВС, АВ ⊥ АD) – трапеция,
АD = 24 см, ВС = 16 см, 
DВ – биссектриса кута D, 
СК – высота трапеции. 
∠ ADB = ∠ CDB, так как 
DВ – биссектриса угла  D, 
∠ ADB = ∠ DBC, так как 
АD ∥ ВС  и  DВ – секущая.
Тогда, ∠ DBC = ∠ CDB  и треугольник  ВСD – равнобедренный,
СD = СВ = 16 см,
КD = АD – АК = 
= АD – ВС =
= 24 – 16 = 8 см.
Из треугольника  СКD (∠ К = 90°)  получим:

S = 1/2(АD + ВС)× СК 

= 1/2(24 + 16)× 8√͞3 
= 160√͞3 см2.

ЗАДАЧА:

В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторону на отрезки длиной  4 см  и  9 см. Найдите площадь трапеции.

Пусть  АВСD (АD ∥ ВС, СD ⊥ АD) – прямоугольная трапеция, в которую вписана окружность с центром  О.
Е, F, К, Р – точки касания окружности до сторон трапеции.
АР = АЕ = 9 см  как касательные к окружности, проведённые из одной точки. Аналогично  

ВF = ВЕ = 4 см. 
Проведём 
ВL ⊥ АD,  ОF ⊥ ВС,  ОР ⊥ АD 

как радиусы, проведённые к касательным.
Поэтому, FР ⊥ АD, откуда 

LР = ВF = 4 см,
АL = АР – ВF 
= 9 – 5 = 4 см.

Из треугольника  АВL:
СD = ВL = 12 см. 
ОР = ОF  как радиусы окружности.
РОКD  і  ОFСК – квадраты, у которых общая сторона  ОК, поэтому
СК = КD = 1/2 ВL 
= 1/2 12 = 6 см.
Откуда  
FС = РD = 6 см. 
Поэтому,
ВС = ВF + FС 
= 4 + 6 = 10 см.
АD = АР + РD 
= 9 + 6 = 15 см.
S = 1/2 (ВС + АD)×СD
= 1/2 (10 + 15)×12 = 150 см2.

ЗАДАЧА:

Большая диагональ прямоугольной трапеции делит высоту, проведённую из вершины тупого угла, на отрезки длиной  15 см  и  9 см, а большая боковая сторона трапеции равна её меньшему основанию. Найдите площадь трапеции.

РЕШЕНИЕ:

Пусть  АВСD – прямоугольная трапеция  (АВ ⊥ ВС, АВ ⊥ АD),
∠ ВСD – тупой. Тогда  СК – высота, проведённая из вершины этого угла, делится диагональю  ВD  на отрезки

СМ = 15 см, МК = 9 см.

Так как по условию  ВС = СD, то треугольник  ВСD – равнобедренный. Тогда

∠ СВD = ∠ СDВ (1).

Прямые  ВС  и  АD  параллельные, поэтому

∠ СВD = ∠ ВDА (2)

 как внутренние разносторонние при секущей  ВD. Из равенств  (1)  и  (2)  получим, что  ∠ СDВ = ∠ ВDА. Поэтому, DВ – биссектриса  ∠ СDА  трапеции.

Из треугольника  СDК  по свойству биссектрисы получим:
Пусть  СD = 5х, тогда  DК = 3х.

Из  ∆ СDК (∠ К = 90°):

СD2 = СК2 + КD2,

25х2 = 242 + 9х2,

16х2 = 242, 4х = 24,

х = 6 см.

Получим:

СD = 5 ∙ 6 = 30 (см),

DК = 3 ∙ 6 = 18 (см).

ВС = СD = 30 см,

АD = АК + КD =

= ВС + КD =

= 30 + 18 = 48 (см).

Sтр. = 1/2 (АD + ВС)∙ СК =

= 1/2 (30 + 48) ∙ 24 = 

= 78 ∙ 12 = 936 (см2).

ОТВЕТ:  936 см2

ЗАДАЧА:

У прямоугольную трапецию  АВСD (АD ∥ ВС, АВ ⊥ АD)  вписана окружность с центром в точке  О. Найдите площадь трапеции, если 

ОС = 6 см, ОD = 8 см.

РЕШЕНИЕ:

Начертим чертёж.
Очевидно, что  ∆ СОD  прямоугольный с катетами  6 см  и  8 см. Тогда  СD = 10 см. Точка  К – точка касания касательной  СD  до окружности.

ОК  ⊥ СD, ОК = R,

ВС = R + МС (МС = КС),

АD = R + ND, (ND = КD),

SABCD = ВС∙ АD,

2S∆COD = ОС∙ ОD =

= СD∙ R,

6 ∙ 8 = 10∙ R,

R = 4,8 см.

Воспользуемся следующими соотношениями в прямоугольном  ∆ СОD:

ОС2 = СD∙ СК, 

36 = 10∙ СК,

СК = МС = 3,6 см.

Тогда  КD = ND =

= 10 – 3,6 = 6,4 (см).

SABCD = (4,8 + 3,6) ∙ (4,8 + 6,4) =

= 94,08 (см2).

ОТВЕТ:  94,08 (см2)

Задания к уроку 11
Другие уроки:
на

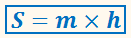
Комментариев нет:

Отправить комментарий