ВІДЕОУРОК
Кульовою поверхнею або сферою називається геометричне місце точок простору, рівновіддалених від однієї точки, що зветься центром сфері.
АО = ОВ = R.
Хордою сфери називається відрізок прямої, який сполучає дві її будь-яки точки.
Діаметром сфери називається хорда, що проходить через її центр, наприклад АС або ВD. Кінці будь-якого діаметра називаються діаметрально протилежними точками кулі.
Кулею називається тіло, обмежене сферою.
Переріз сфери і кулі площиною.
Переріз сфери будь-якою площиною є коло.
Переріз кулі будь-якою площиною є круг.
Круг, утворений перерізом кулі площиною, яка проходить через центр, називається великим кругом кулі, а круг, утворений перерізом кулі площиною, яка не проходить через центр, називається малим кругом кулі. Перерізи рівновіддалені від центра кулі, рівні між собою.
Будь-яка площина, що проходить через центр кулі, ділить його поверхню на дві симетричні і рівні частини.
Через дві точки сфери, які не лежать на кінцях одного діаметра, можна провести коло великого круга, і до того ж тільки одне.
Кола двох великих кругів при перетині діляться пополам.
Площина, дотична до кулі.
Дотичною площиною до кульової поверхні називається площина, що має з нею поверхнею тільки одну спільну точку.
Площина, перпендикулярна до радіуса кульової поверхні в його кінці, що лежить на цієї поверхні, є дотичною площиною.
Обернено:
Дотична площина перпендикулярна до радіуса, проведеного в точку дотику.
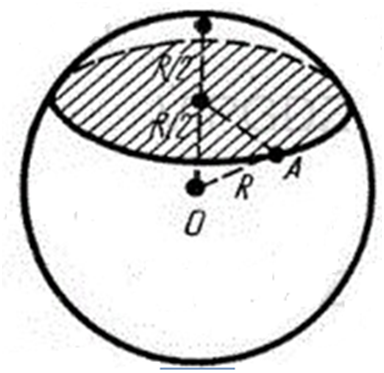
ЗАДАЧА:
Через
середину радіусу кулі проведено перпендикулярну радіусу площину. Як відноситься
площа отриманого перерізу до площі великого кола
?
РОЗВ'ЯЗАННЯ:
Частини на кульової поверхні, що відтинається від неї якою-небудь площиною, називається сегментною поверхнею.
Поверхня кульового сегмента, пояса і кулі.
За величину поверхні кульового сегмента, пояса і кулі, утвореної обертанням якої-небудь частини півкола або всього півкола навколо діаметра, приймають границю, до якої наближається поверхня, утворена обертанням навколо того самого діаметра правильної вписаної ламаної лінії у відповідну частину дуги кола при необмеженому збільшенні числа її сторін.
Де R – радіус великого круга кулі, а Н – висота сегментної поверхні.
ЗАДАЧА:
РОЗВ'ЯЗАННЯ:
Для
знаходження площі поверхні котла потрібно знайти площі поверхонь двох сферичних
сегментів та площу поверхні циліндричної частини котла.
Визначимо
радіус сфери, частинами якої є поверхні сегментів, навіщо побудуємо центр сфери
– точку О.
З
прямокутного трикутника MON маємо:
R2 = r2 + (R – h1)2, або
S = 2πrh + 4πRh1 = 2π(rh
+ 2Rh1).
Замінивши
в цій рівності R, r, h та
h1 їх даними значеннями, отримаємо:
S
= 6,28(0,6 ∙ 2 + 2 ∙ 1 ∙ 0,2) ≈ 10,05 м2.
Помноживши
вагу 1
м2
листового
заліза на число квадратних метрів поверхні котла, отримуємо його вагу:
Р
= 12 ∙ 10,05 = 120,6 ≈ 121 (кг).
Де R – радіус кола великого круга, а Н – висота пояса.
Площа поверхні кули.
Дамо наступне
визначення площі поверхні кулі:
За площу
поверхні кулі, отриманого обертанням півкола навколо діаметра, приймається
межа, якого прагне поверхня, одержувана обертанням біля того ж діаметра
правильної вписаної в півколо ламаної лінії при необмеженому збільшенні числа
її ланок.
Де R – радіус кулі.
Поверхні куль відносяться, як квадрати їх радіусів або діаметрів.
Кульовий сегмент, шар і сектор.
Кульовим сегментом називається тіло, яке відтинає площина від кулі.
Кульовим шаром називається тіло, яке відтинається від кулі двома паралельними січними площинами.
Кульовим сектором називається тіло, одержане від обертання кругового сектора навколо осі, що лежить в його площині, яка проходить через його центр і не перетинає сектора.
Дотична площина до кулі.
Площина, що проходить через точку А кульової поверхні й перпендикулярна радіусу, проведеному в точку А, називається дотичною площиною. Точка А називається точкою дотику.
ЗАДАЧА:
Сторони трикутника дорівнюють
15, 14 і 13 см.
Знайти віддаль від площини трикутника до центра кулі, дотичної до сторін трикутника, якщо радіус кулі дорівнює 5 см.
АВ = 15 см,
ВС = 14 см,
АС = 13 см.
Знайти віддаль від центра кулі до площини ∆ АВС.
Площина ∆ АВС перетне кулю О по кругу, вписаному в даний трикутник. Основа перпендикуляра ОD, опущеного з центра кулі О на площину ∆ АВС, попадає в центр круга D.
Радіус кулі R = ОМ = 5 см. Радіус круга D, вписаного в даний трикутник, знайдемо за формулою
де S – площа, а р – півпериметр трикутника:
Підставляючи знайдені значення у формулу для ОD, знаходимо шукану віддаль
ВІДПОВІДЬ: 3 см.
ЗАДАЧА:
Радіуси двох сфер дорівнюють 10 см і 17 см, а довжина лінії їх перетину – 16π см. Знайдіть відстань між центрами сфер.
Дано:
ОА = 10 см,
О1А = 17 см.
Спер = 16π см.
Знайти: ОО1.
16π = 2πr;
r = 8 см;
О2А = 8 см.
∆ОАО2 – прямокутний,
∆О1АО2 – прямокутний,
ВІДПОВІДЬ: 21 см.
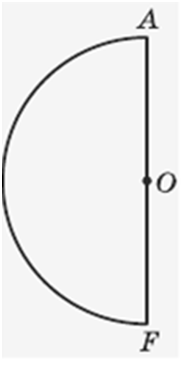
За умовою задачі
CD = h, ∠ AOB = α.
Знайти площу сферичної поверхні сегмента (на рисунку дано його переріз).
Площа сферичної поверхні сегмента
або звідки Підставивши це значення у формулу для S, після очевидних спрощень одержимо остаточну відповідь: ВІДПОВІДЬ: Завдання до уроку 16
- Урок 1. Прямі і площині у просторі
- Урок 2. Пряма призма
- Урок 3. Похила призма
- Урок 4. Правильна призма
- Урок 5. Паралелепіпед
- Урок 6. Прямокутний паралелепіпед
- Урок 7. Куб
- Урок 8. Піраміда
- Урок 9. Правильна піраміда
- Урок 10. Зрізана піраміда
- Урок 11. Циліндр
- Урок 12. Вписана і описана призма
- Урок 13. Конус
- Урок 14. Зрізаний конус
- Урок 15. Вписана і описана піраміда
- Урок 17. Комбінації тіл
































Комментариев нет:
Отправить комментарий