Урок 2. Пряма призма

суббота, 14 октября 2017 г.

Урок 2. Пряма призма

ВІДЕОУРОК

Багатогранні кути.

Багатограннім кутом називається фігура, яка складається з кількох променів ОА, ОВ, ОС, …, ОF, що виходять з однієї точки О і не лежать в одній площині, і з плоских кутів АОВ, ВОС,…, FОА між цими променями.

Спільна точка О перетину всіх променів називається вершиною багатогранного кута, промені ОА, ОВ, ОС, …, ОF – його ребрами, частини площини, що лежать між ребрами, називаються його гранями, а кути АОВ, ВОС,…, FОА, утворені ребрами, що лежать в одній грані, називаються плоскими кутами багатогранного кута.

Багатогранний кут називається опуклим, якщо він повністю лежить по один бік від площини, яка суміщається з будь-якою його гранню.

Два багатогранні кути вважаються рівними, якщо вони при накладанні суміщаються усіма своїми частинами.

Сума плоских кутів опуклого багатогранного кута менша за 360°.

Тригранні кути.

Якщо число граней багатогранного кута дорівнює трьом, то його називають тригранним.

Основні властивості тригранних кутів:

– сума двох плоских кутів тригранного кута більша за третій його плоский кут;

– кожний плоский кут тригранного кута більший за різницю двох інших його плоских кутів.

Рівними тригранними кутами називаються такі кути, які при накладанні суміщаються всіма своїми частинами.

Отже, у рівних тригранних кутів всі двогранні і плоскі кути відповідно рівні між собою, але обернене твердження неправильне. Існують такі тригранні кути, у яких двогранні і плоскі кути відповідно рівні, а тригранні кути не рівні між собою.

ПРИКЛАД:

На рисунку зображено два тригранні кути, у яких плоскі і двогранні кути відповідно рівні, а сумістити їх неможливо.

Тригранні кути неможливо сумістити, тому що їх відповідні грані неоднакові орієнтовані відносно вершини. Грані АОВ, ВОС і СОА орієнтовані відносно вершини О проти руху годинникової стрілки, а відповідні грані А₁ОВ₁, В₁ОС₁ і С₁ОА₁ – за рухом годинникової стрілки, і тригранні кути і не рівні, хоча в них рівні і всі плоскі і всі двогранні кути. Таким чином, для рівності двох тригранних кутів з відповідно рівними плоскими і двогранними кутами необхідно також, щоб їх грані були однаково орієнтовані відносно їх вершин.

Ознаки рівності тригранних кутів.

Існують ознаки рівності тригранних кутів, аналогічні до ознак рівності трикутників в планіметрії.

– якщо два однаково орієнтовані тригранні кути мають по рівному плоскому куту, що лежить між двома відповідно рівними двогранними кутами, то такі тригранні кути рівні;

– якщо два однаково орієнтовані тригранні кути мають по два рівні плоскі кути, площини яких утворюють рівні двогранні кути, то такі тригранні кути рівні;

– якщо два однаково орієнтовані тригранні кути мають по три відповідно рівні плоскі кути, то такі тригранні кути рівні;

– якщо два тригранні кути однаково орієнтовані і мають по три відповідно рівні двогранні кути, то такі тригранні кути рівні.

Основні визначення.

Багатогранником називається геометричне тіло, поверхня якого складається з частин площин, обмежених багатокутниками.

Гранями багатогранника називаються частини площин (багатокутники), які обмежують багатогранник.

Ребрами багатогранника називаються спільні сторони суміжних граней (багатокутників).

Вершинами багатогранника називаються вершини багатогранних кутів, утворених його гранями, що сходяться в одній точці.

Діагоналлю багатогранника називається відрізок прямої, яка сполучає дві вершини багатогранника, що не лежать в одній грані.

Діагональною площиною багатогранника називається площина, що проходіть через три вершини багатогранника, які не лежать в одній грані.

Перерізом багатогранника площиною називається частина цієї площини, яка обмежена лінією перетину поверхні багатогранника з цією площиною.

Багатогранник називається опуклим, якщо він цілком лежіть по одну сторону від площини будь-якої його грані.

Гранями опуклого багатогранника можуть бути тільки опуклі багатокутники.

Для кожного опуклого багатогранника

Сума числа вершин В і числа граней Г на 2 більша за число його ребер Р:

В + Г – Р = 2.

Призма.

Призмою називається багатогранник, дві грані якого паралельні, а інші перетинаються по паралельних прямих.

Грань, на якій <<стоїть>> призма, та протилежна її грань називаються основами призми, а всі інші – бічними гранями.

З визначення випливає, що в основах призми лежать рівні многокутники з відповідно паралельними сторонами, а бічні грані призми – паралелограми.

Спільні сторони бічних граней призми називаються бічними ребрами.

Відрізок ОО₁ прямої, перпендикулярний до площин основ призми, що лежить між ними, називається висотою призми.

Діагональною площиною призми прийнято називати площину, яка проходить через діагональ основи і бічне ребро, а фігуру Е₁С₁СЕ

одержану при перетині цієї площини поверхнею призми, називають діагональним перерізом призми.
Діагональний переріз призми – паралелограм.

Переріз призми площиною, перпендикулярною до її бічних ребер, називають перпендикулярним перерізом призми.

На рисунку фігура A₂B₂C₂D₂E₂ є перпендикулярним перерізом призми.

n-кутна призма має 2n вершин, n + 2 граней, 3n ребер.

Пряма призма.

Призма називається прямою, якщо її бічні ребра перпендикулярні до площини основи.

У прямий призмі висота ОО₁ паралельна до всіх її бічних ребер

АА₁, ВВ₁, СС₁…

Усі бічні ребра прямої призми рівні між собою. Кожне з них є висотою прямої призми. Усі бічні грані – прямокутники.

Пряма призма називається:

трикутною,

чотирикутною,

п'ятикутною

і т. д. в залежності від того, який многокутник лежить в її основі.

Поверхня прямій призми.

Бічною поверхнею прямій призми називається сума площ всіх її бічних граней.

Повною поверхнею прямій призми називається сума її бічної поверхні і площ основ.

Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми.

Розглянемо пряму трикутну призму та її розгортку.

Нехай довжини сторін трикутника, що лежить в основі призми, дорівнюють

ВС = а, АС = b, АВ = с,

а довжина бічних ребер

АА₁, ВВ₁, СС₁ – H.

Тоді площа бічної поверхні цієї призми:

S_б = аH + bH + сH =

(а + b + с)H = РH,

де Р – периметр трикутника, що лежить в основі.

ЗАДАЧА:

За даною на рисунку розгорткою прямої трикутної призми (розміри задано в сантиметрах) знайти площі її бічної і повної поверхонь.

Площу бічної поверхні призми знаходимо за формулою

S_б = PH,

де P = 5 + 8 + 5 = 18 (cм),

Н = 12 см,

S_б =18 × 12 = 216 (см)².

Площа повної поверхні призми дорівнює сумі площі бічної поверхні та площ двох трикутників, які є основами.

де a = 8 cм, h = 3 cм.

Виконаємо обчислення:

Отже,

S_п = 216 + 12 × 2 = 240 (см)².

ЗАДАЧА:

Основою прямої призми є ромб з тупим кутом 150°. Площа бічної поверхні призми дорівнює 96 см², а площа її повної поверхні – 132 см². Знайти висоту призми.

РОЗВ'ЯЗАННЯ:

Нехай ABCDA₁B₁C₁D₁– пряма призма, ABCD – ромб,

∠ ADC = 150°,
S_б = 96 см²,
S_п = 132 см².

S_п – S_б = 2S_ABCD =
132 – 96 = 36 (см²),

звідки S_ABCD = 18 (см²).

Отже,
S_ABCD = AD² × sin ∠ ADC.

Звідки

S_б = 4AD × DD₁, звідки

ВІДПОВІДЬ: 4 см

ЗАДАЧА:

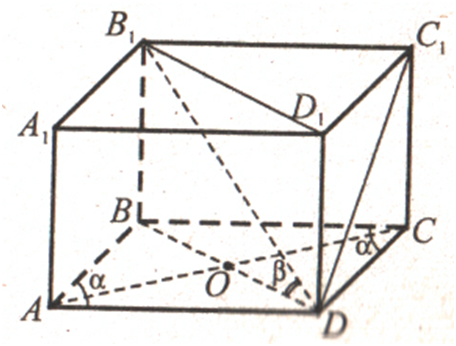
Основа прямої призми – ромб з гострим кутом α. Діагональний переріз призми, що проходить через більшу діагональ основи, має площу S. Знайдіть площу бічної поверхні призми.

РОЗВ'ЯЗАННЯ:

Нехай АВСDА₁В₁С₁D₁ – задана призма.
АВСD – ромб, ∠ С = ∠ А = ∠ α – гострий. Тоді АС – більша диагональ ромба. AА₁C₁C – заданий діагональний переріз і
Нехай сторона ромба дорівнює а. За властивістю діагоналей ромба

∠ ACD = ^α/₂. DO ⊥ (OCC₁), оскільки

OD ⊥ OC і OD ⊥ OO₁.

Аналогічно D₁O₁ ⊥ (O₁C₁C). Таким чином, проекцією грані DD₁C₁C на заданий діагональний переріз є чотирикутник OO₁C₁C. (площа якого дорівнює ^S/₂). Кут між цими площинами дорівнює ^α/₂

(DC ⊥ CC₁, OC ⊥ CC₁, ∠ DCO = ^α/₂). Тому
ВІДПОВІДЬ:
ЗАДАЧА:

Основа прямої призми – ромб з гострим кутом α, площа якого дорівнює S. У призмі проведено діагональний переріз, що проходить через меншу діагональ основи. Діагональ цього перерізу нахилена до площини основи під кутом β. Знайдіть площу бічної поверхні призми.

РОЗВ'ЯЗАННЯ:

Нехай ABCDA₁B₁C₁D₁– задана призма.
АВСD – ромб,

∠ С = ∠ А = ∠ α – гострий. Тоді ВD – менша діагональ ромба.

BDD₁C₁ – діагональний переріз. Відрізок ВD – проекція діагоналі B₁D на площину основи. Тому ∠ B₁DВ – кут нахилу діагоналі B₁D до площини основи. За умовою,