Урок 8. Піраміда

ВІДЕОУРОК

Предмети мають особливу форму – піраміди. Головоломка Рубіка є прикладом трикутної піраміди, а об’ємний пазл – чотирикутної піраміди.

Многогранник, одна з граней якого – довільний многокутник, а решта граней – трикутники, що мають спільну вершину, називається пірамідою.

Обмежують піраміду її грані. Ви бачите, що у трикутної піраміди всі грані є трикутниками, а в чотирикутної – не всі. Одна грань є чотирикутником. У загалі, у піраміди одна грань може бути яким завгодно многокутником. Така грань називається основою піраміди. Решта граней обов'язково є трикутниками. Вони називаються бічними гранями піраміди. Називають піраміду залежно від того, який многокутник є її основою. Якщо основа – трикутник, піраміда називається трикутною, якщо чотирикутник – чотирикутною, якщо  n – кутник – n – кутною. Як і грани, вершини піраміди теж мають свої назви. Вершину, в якій сходяться бічні грані піраміди, називають вершиною піраміди, а решту вершин – вершинами її основи. Вершина піраміди завжди лежить проти основи піраміди. Міркуючи аналогічно, дістанемо, що у піраміди є бічні ребра і ребра основи. Бічні ребра, як і бічні грані, сходяться у вершині піраміди. Вони сполучають вершину піраміди з вершинами основи. Позначають піраміду назвами її вершин, наприклад, SABCD. Першою завжди записують вершину піраміди.

На відміну від прямокутного паралелепіпеда і куба, кількість вершин, ребер і граней не є однаковою для всіх пірамід, а залежить від того, якого виду піраміда.

Висотою піраміди називається перпендикуляр  SО, опущений з вершини піраміди на площину – її основи.

Зауважимо, що в піраміді буквою  S  звичайно позначають і її вершину і поверхню (повну або окремих її частин). Але це не призводить до непорозумінь, бо за змістом завжди ясно, про що йдеться в даному випадку. Крім того, якщо розглядають поверхню або площу, то в позначення часто ще вводять додаткові індекси, наприклад  S_бічн  (бічна поверхня), S_ABCD (площа основи  ABCD),  S_ASB (площа грані  ASB) і т. ін.

Властивості перерізів піраміди площиною, паралельною до основи.

Якщо піраміду перетнути площиною, паралельною до основи, то:

– бічні ребра і висота піраміди діляться цією площиною на пропорціональні відрізки;

– в перерізі одержуємо многокутник, подібний до многокутника, що лежить в основі;

– площі перерізу і основі відносяться між собою, як квадрати їх віддалей від вершини піраміди.

На рисунку зображено піраміду  SABCD  і паралельні площини   A₁B₁C₁D₁ ∥ ABCD

В такому випадку

Многокутник  A₁B₁C₁D₁  подібний до многокутника  ABCD;

Якщо дві піраміди з рівними висотами перерізати площинами, паралельними до основ, на однаковій віддалі від вершини, то площі перерізів будуть пропорціональні до площ основ.

На рисунку зображено піраміді

Висоти яких рівні:

На однакових віддалях від вершин

проведено площини

паралельні до основ пірамід. Тоді

Якщо у двох пірамідах з рівновеликими основами і рівними висотами провести паралельні до основ перерізи на однакових віддалях від вершини, то перерізи будуть рівновеликими.

Поверхня піраміди.

Бічною поверхнею піраміді називається сума її бічних граней.

Повною поверхнею піраміди називається сума її бічної поверхні і площі основи.

Площа повної поверхні піраміди обчисляється за формулою:

S_пір = S_бічн + S_осн

Якщо трикутники, що утворюють бічну поверхню піраміди, не рівні, то для знаходження бічної поверхні піраміди треба знайти площу кожного трикутника і ці площі додати.

ЗАДАЧА:

Основою піраміди є квадрат, її висота проходіть через одну з вершин основи. Визначити бічну поверхню цієї піраміди, якщо сторона основи дорівнює  20 дм, а висота – 21 дм.

Дано піраміду  SABCD, в основі якої лежить квадрат  ABCD  з стороною  20 дм, висота  SD = 21 дм.

РОЗВ'ЯЗАННЯ:

Визначити бічну поверхню піраміди.

Бічна поверхня піраміди дорівнює сумі площ бічних граней:

S_бічн = S_ASD + S_DSC + S_CSB + S_BSA.

∆ASD  і  ∆CSD – прямокутні і рівні, а їх площі

S_ASD = S_CDS = ¹/₂ ×20×21 = 210 (дм²).

З цих трикутників за теоремою Піфагора знаходимо

Оскільки за теоремою про три перпендикуляри

SC ⊥ CB ⊥ SA ⊥ AB (DC ⊥ CB ⊥ DA ⊥ AB),

то  ∆SAB  і  ∆SCB – прямокутні і рівні, і їх площі

S_ASB = S_CSB =
¹/₂ ×20×29 = 290 (дм²).

тоді

S_бічн = 2(290 + 210) 
= 1000 (дм²).

ВІДПОВІДЬ;

1000 дм² = 10 м². 

ЗАДАЧА:

Основа піраміди – квадрат зі стороною  12 см, а дві сусідні бічні грані перпендикулярні до площини  основи. Обчисліть площу бічної поверхні піраміди, якщо її висота дорівнює  5 см.

РОЗВ'ЯЗАННЯ:

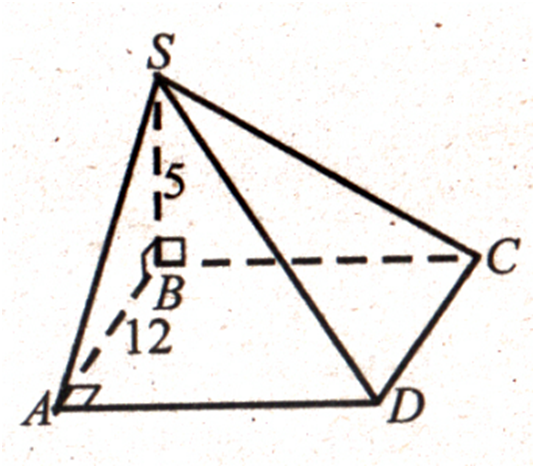
Нехай  SABCD – задана піраміда.

Основа  ABCD – квадрат, АВ = 12 см. Грані  SAB  і  SBC  перпендикулярні до площини основи. Тоді їх спільне ребро  SB  є висотою піраміди. За умовою, SB = 5 см.

З  ∆ SBА (∠ В = 90°):

Оскільки  BА ⊥ АD, то за теоремою про три перпендикуляри  SA ⊥ АD. Аналогічно  SС ⊥ DС.

∆ SBС = ∆ SBА, ∆ SАD = ∆ SСD,

(за двома катетами).

S_б = 2S_{∆ SBА} + 2S_{∆ SAD}.

S_{∆ SАD} = ¹/₂ SA ∙ AD = ¹/₂ ∙ 13 ∙ 12 = 78 (см²).

S_{∆ SBA} = ¹/₂ SB ∙ AB = ¹/₂ ∙ 5 ∙ 12 = 30 (см²).

S_б = 2 ∙ 78 + 2 ∙ 30 = 216 см².

ВІДПОВІДЬ:  216 см²

ЗАДАЧА:

Основа піраміди – квадрат зі стороною  9 см, а дві сусідні бічні грані перпендикулярні до площини  основи. Обчисліть площу бічної поверхні піраміди, якщо середнє за довжиною бічне ребро піраміди дорівнює  15 см.

РОЗВ'ЯЗАННЯ:

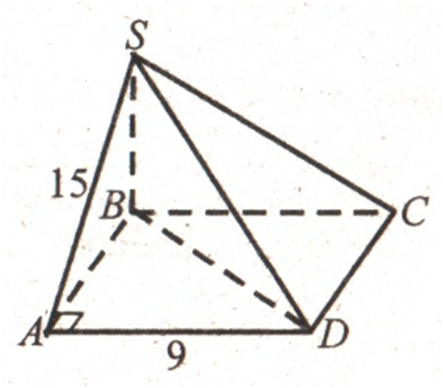
Нехай  МABCD – задана піраміда. Основа  ABCD – квадрат,

АВ = 9 см. Грані  SBA  і  SBC  перпендикулярні до площини основи. Тоді їх спільне ребро  SB  є висотою піраміди і є найкоротшим. Проекціями ребер  SA  і  SC  на площину основи є сторони, а ребро  SD – діагональ квадрата. Оскільки  BD ˃ AB, то  SD ˃ SA. Ребра  SA  і  SC – середні за довжиною ребра піраміди. SА = SС = 15 см. Оскільки  ВА ⊥ АD, то за теоремою про три перпендикуляри  SА⊥  АD. Аналогічно  SC ⊥ DC.

∆ SAD = ∆ SCD,

∆ SBC = ∆ SBA.

(за двома катетами).

S_б = 2S_{∆ SAD} + 2S_{∆ SBA}.

S_{∆ SAD} = ¹/₂ SA ∙ AD =

= ¹/₂ ∙ 15 ∙ 9 = ¹³⁵/₂ (см²).

З  ∆ SBА (∠ В = 90°):

S_{∆ SBA} = ¹/₂ SB ∙ AB =

= ¹/₂ ∙ 12 ∙ 9 = 54 (см²).

S_б = 2 ∙ ¹³⁵/₂ + 2 ∙ 54 =

= 135 +108 = 243 (см²).

ВІДПОВІДЬ:  243 см²

ЗАДАЧА:

Основа піраміди – прямокутник зі сторонами  6 см  і  15 см, а дві сусідні бічні грані перпендикулярні до площини основи. Обчисліть площу бічної поверхні піраміди, якщо її висота дорівнює  8 см.

РОЗВ'ЯЗАННЯ:

У піраміді  МABCD  основа  ABCD – прямокутник,

бічні грані  ABМ  і  СBМ  перпендикулярні до площини прямокутника  ABCD. Тоді їх спільне бічне ребро  МВ  є висотою піраміди,

МВ = 8 см, АВ = 6 см, ВС = 15 см.

Відрізок  АВ – проекція відрізка  АМ  на площину основи,  АВ ⊥ AD. Тоді  МА ⊥ AD. Аналогічно, доводимо, що  МС ⊥ AD.

З  ∆ АBМ (∠ В = 90°):

З  ∆ СBМ (∠ В = 90°):

S_{∆ ABM} = ¹/₂ AB ∙ MB = 24 (см²),

S_{∆ CBM} = ¹/₂ BC ∙ MB = 60 (см²),

S_{∆ MAD} = ¹/₂ AD ∙ MA = 75 (см²),

S_{∆ MCD} = ¹/₂ CD ∙ MC = 51 (см²).

Площа бічної поверхні піраміди:

S = S_{∆ ABM}  + S_{∆ CBM}  + S_{∆ MAD}  + S_{∆ MCD} =

= 24 + 60 + 75 + 51 = 210 (см²).

ВІДПОВІДЬ:  210 см²

Розв'язання задач із стереометрії за допомогою тригонометрії.

ЗАДАЧА:

Основа піраміди  SABCD є квадрат  ABCD. Бічна грань  ASB  перпендикулярна до площини основи, грані  ASD  і  BSC  нахилені до площини основи під кутом  60°. Знайдіть кут нахилу грані  СSD  до площини основи.

РОЗВ'ЯЗАННЯ:

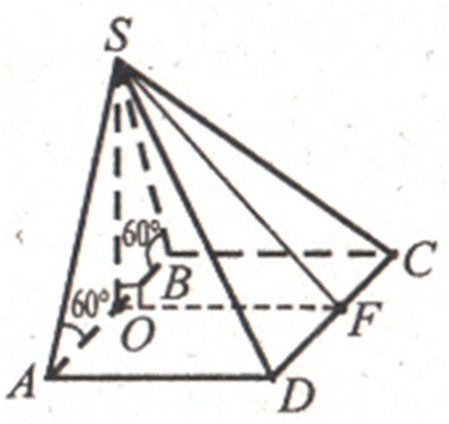
Нехай  SABCD – задана піраміда. ABCD – квадрат.

Оскільки грань  ASB  перпендикулярна до площини основи, то висота  SO  належіть цій грані. OB ⊥ BС. За теоремою про три перпендикуляри  SB ⊥ BС. Тоді  ∠ SBO – кут нахилу грани  BSC  до площини основи. Аналогічно  ∠ SAO – кут нахилу площини  ASD  до площини основи. Тому ∠ SAO = ∠ SBO = ∠ 60°. Отже, трикутник  ASВ  рівносторонній, у якому висота  SO  є й медіаною. Проведемо  SF ⊥ DС, тоді  OF ⊥ DС, а отже, OF ∥ DA, OF = AD. Тоді ∠ SFO – кут нахилу грані  CSD  до площини основи. З  ∆ SOA (∠ O = 90°):

З  ∆ SOF (∠ O = 90°):

ВІДПОВІДЬ:

ЗАДАЧА:

Основою піраміди  МABCD  є квадрат  ABCD. Бічна грань  BМС  перпендикулярна до площини основи, грань  AМD  нахилена до площини основи під кутом  30°, грані  АМВ  і  СМD  утворюють з площиною основи рівні кути. Знайдіть кут нахилу грані  АМВ  до площини основи.

РОЗВ'ЯЗАННЯ:

Нехай  МABCD – задана піраміда. ABCD – квадрат.

Оскільки грань  BMC  перпендикулярна до площини основи, то висота  MO  належіть цій грані. OB ⊥ AB. За теоремою про три перпендикуляри  MB ⊥ AB. Тоді  ∠ MBO – кут нахилу грани  AMB  до площини основи. Аналогічно  ∠ MCO – кут нахилу площини  CMD  до площини основи. За умовою  ∠ MBO = ∠ MCO, а тому трикутник  ВМС –   рівнобедрений і  МО  є висотою і медіаною. Проведемо  MF ⊥ AD. Тоді  OF ⊥ AD, а отже, OF ∥ AB, OF = AB. Тоді ∠ MFO – кут нахилу грані  AMD  до площини основи. За умовою, ∠ МFO = 30°. Нехай  АВ = а.
З  ∆ MOF (∠ O = 90°):

Звідки

З  ∆ MOB (∠ O = 90°):

Звідки

 

ВІДПОВІДЬ:

ЗАДАЧА:

У трикутній піраміді  ABCD  ребро

CD ⊥ AD, CD ⊥ BD, CD = 1,

двогранний кут при ребрі  CD  дорівнює 120°, а

AD = BD = √͞͞͞͞͞2.

Знайдіть величину двогранного кута при ребрі  АВ.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.

Відрізок CD перпендикулярний двом прямим  BD  і  AD  площині  ABD, що перетинаються, а значить, CD  перпендикулярний площині  ABD.  ∠ ADB = 120°, ∆ ADB – рівнобедрений.
Потрібно знайти величину двогранного кута при ребрі  АВ. Для цього треба знайти лінійний кут цього двогранного кута, а сторони лінійного кута перпендикулярні до  АВ. Побудуємо точку  К – середину ребра  АВ  та з'єднаємо її з точками  С  і  D.

DК – медіана  ∆ ADB, отже, і висота. КВ ⊥ СК.

∠ СКD – лінійний кут двогранного кута при ребрі  АВ.

Розглянемо трикутник  DКВ, він прямокутний, кут  DВК = 30°, а проти кута в  30°  лежить катет рівний половині гіпотенузи, значить

Звідки  ∠ CKD = arctg√͞͞͞͞͞2

ВІДПОВІДЬ:  arctg√͞͞͞͞͞2

Завдання до уроку 8

• Завдання 1
• Завдання 2
• Завдання 3

Інші уроки:

• Урок 1. Прямі і площині у просторі
• Урок 2. Пряма призма
• Урок 3. Похила призма
• Урок 4. Правильна призма
• Урок 5. Паралелепіпед
• Урок 6. Прямокутний паралелепіпед
• Урок 7. Куб
• Урок 9. Правильна піраміда
• Урок 10. Зрізана піраміда
• Урок 11. Циліндр
• Урок 12. Вписана і описана призма
• Урок 13. Конус
• Урок 14. Зрізаний конус
• Урок 15. Вписана і описана піраміда
• Урок 16. Сфера і куля
• Урок 17. Комбінації тіл