ВИДЕО УРОК
Для решения косоугольного треугольника существует теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.Рассмотрим отдельно три возможных случая.1. Пусть угол А – острый.Из геометрии известно, что
квадрат стороны
треугольника, лежащей против острого угла, равен сумме квадратов двух других
сторон без удвоенного произведения одной из этих сторон на отрезок её от
вершины острого угла до высоты.
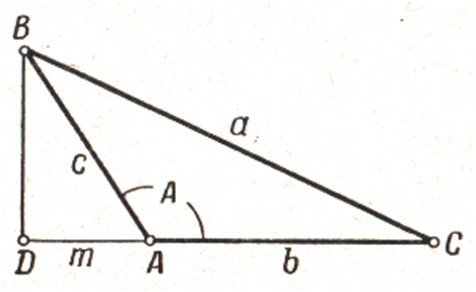
Пусть
ВD ⊥ АС, АD
= m.
Тогда
a2 = b2 + с2
– 2bm.
Из прямоугольного
треугольника АВD находим:
m = с cos A.
Подставляем в
предыдущее равенство вместо m равное ему выражение с cos A, получим следующее равенство:
a2 = b2
+ с2 – 2bс cos A.
Выведем теорему косинусов, когда сторона треугольника лежит против острого
угла, вторым способом.
bc = b cos α.
Окончательно имеем:
a2 = b2
+ с2 – 2bс cos α,
что и требовалось доказать.
a2 = b2 + с2
+ 2bm.
Но
m = с cos ∠ DАВ,
и так как ∠ DАВ –
смежный с углом А данного треугольника, то
∠
DАВ =
180° – А.
Следовательно,
cos ∠
DАВ =
cos (180° –
А) = – cos А.
Теперь равенство
m = с cos ∠ DАВ
примет вид
m = – с cos А.
Подставляем
полученное выражение для m в равенство
a2 = b2 + с2
+ 2bm,
будем иметь:
a2 = b2 + с2
+ 2b(–с cos А),
или
a2 = b2 + с2
– 2bс cos А.
Выведем теорему косинусов, когда сторона треугольника лежит против тупого
угла, вторым способом.
bc = b cos (180° – α) = –b cos α.
Окончательно получим:
a2 = b2
+ с2 – 2bс cos α.
Теорема доказана.
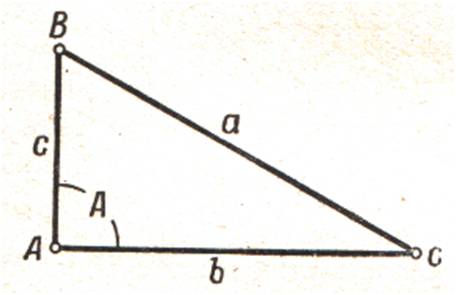
a2 = b2 + с2
– 2bс cos А = b2 + с2.
Но в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
a2 = b2 + с2.
Сравнивая
a2 = b2 + с2
– 2bс cos А = b2 + с2
и
a2 = b2 + с2,
a2 = b2 + с2
– 2bс cos А.
СЛЕДСТВИЕ.
Если две стороны
одного треугольника соответственно равны двум сторонам другого треугольника, а
углы, лежащие между этими сторонами, не равны, то против большего угла лежит и
большая сторона.
Формулапозволяет вычислить длину одной из сторон треугольника по данным длинам двух других сторон и величине угла, лежащего против неизвестной стороны.
Теорема косинусов
может быть записана и для двух других сторон треугольника:
b2 = a2 + с2 – 2aс cos B,
c2 = a2 + b2 – 2ab cos C.
В треугольнике АВС:
АС = 3, ВС
= 5, АВ = 6.
Найти угол, противолежащий стороне АВ.
РЕШЕНИЕ:
∠ АСВ = arccos
(–1/15).
ОТВЕТ: arccos (–1/15)
ЗАДАЧА:
Задан треугольник АВС, длины сторон которого
АС = 17,
ВС = 14, ∠ АСВ = 60°.
Найти длину третьей стороны рассматриваемого
треугольника.
РЕШЕНИЕ:
Согласно теореме косинусов
АВ2 = АС2 + ВС2
– 2 ∙ АС ∙ ВС ∙ cos ∠ АСВ =
= 172 + 142 – 2 ∙ 17 ∙ 14
∙ cos 60° =
= 280 +
196 – 238 = 247.
Тогда
АВ =
√͞͞͞͞͞247.
ОТВЕТ: √͞͞͞͞͞247
ЗАДАЧА:
Одна из сторон треугольника больше другой на 8
см, а угол между ними равен 120°. Найдите периметр треугольника, если длина третьей
стороны равна 28 см.
РЕШЕНИЕ:
Обозначим одну из сторон треугольника как х,
тогда величина другой стороны равна (х + 8) см.
Исходя из теоремы косинусов, получим:
282 = х2 + (х + 8)2 – 2х(х + 8)cos 120°,
784 = х2 +
х2 + 16х + 64 – 2х(х + 8)(–0,5),
784 = 2х2 +
16х + 64 + х(х + 8),
720 = 3х2 +
16х + 8х,
3х2 +
24х – 720 = 0
Таким образом, периметр треугольника равен:
.
ОТВЕТ: 60 см
ЗАДАЧА:
В треугольнике АВС сторона АС равна 7√͞͞͞͞͞3 см, сторона ВС равна 1 см. Угол С равен 150°. Найдите длину стороны
АВ.
РЕШЕНИЕ:
Применим теорему косинусов и соответствующую формулу:
АВ2 = АС2
+ ВС2 – 2∙АС∙ВС ∙ cos С.
АВ2 = (7√͞͞͞͞͞3)2 + 12 – 2(7√͞͞͞͞͞3)cos 150°.
ЗАДАЧА:
В треугольнике АВС сторона ВС =
4 см, сторона АС =
13 см. Угол С между
ними равен
60°. Найдите неизвестную сторону АВ.
РЕШЕНИЕ:
Запишем для неизвестной стороны АВ теорему косинусов:
АВ2 = АС2 + ВС2
– 2 ∙ АС ∙ ВС ∙ cos С.
Подставляя известные
значения сторон и угла, получим:
АВ2 = 42 + 32 – 2∙4∙3 ∙ cos 60°,
АВ2 = 16 + 9 – 24 ∙ 1/2,
АВ2 = 13,
АВ =
√͞͞͞͞͞13.
ОТВЕТ: √͞͞͞͞͞13 см
ЗАДАЧА:
Стороны треугольника равны соответственно 3,
7 и 8 см. Найти угол, лежащий против стороны длинной 7
см.
РЕШЕНИЕ:
Обозначим стороны
треугольника:
АВ = 3, ВС = 7, АС = 8,
ЗАДАЧА:
РЕШЕНИЕ:
то АМ = 3, МВ = 6.
Из треугольника АВС найдём cos В.Из треугольника СВМ по теореме косинусов найдём СМ:
СМ2 = СВ2 + МВ2
– 2∙СВ∙МВ ∙ cos В,
СМ2 = 32 + 62
– 2∙3∙6 ∙ 1/3 = 33,
СМ = √͞͞͞͞͞33.
ДРУГИЕ УРОКИ- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований




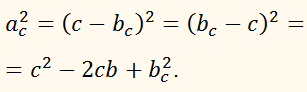



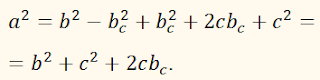
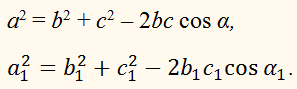






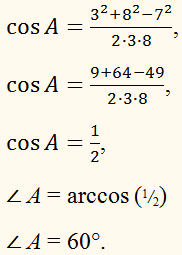

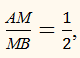


Комментариев нет:
Отправить комментарий