ВИДЕО УРОК
arcsin x = α.
Из этого равенства
следует, что
sin α = x и – π/2 ≤ α ≤ π/2.
Но cos (π/2 – α) также равен
х, так как
cos (π/2 – α) = sin α.
На основании этого
имеем:
cos (π/2 – α) = x.
Но –α заключено в том
же промежутке, что и α:
– π/2 ≤ –α ≤ π/2.
Прибавляя по π/2 ко всем членам
этого соотношения, получим
0 ≤ π/2 – α ≤ π.
Из соотношений
cos (π/2 – α) = x,
0 ≤ π/2 – α ≤ π
следует, что
arccos x = π/2 – α.
Складывая почленно
равенства
arcsin x = α,
arccos x = π/2 – α,
получим:
arcsin x + arccos x = π/2,
что и требовалось
доказать.
arctg x = α,
находим:
tg α = x и – π/2 < α < π/2.
Но ctg (π/2 – α) также равен
х, так как
ctg (π/2 – α) = tg α.
Из неравенства
– π/2 < α < π/2
следует:
0 ≤ π/2 – α ≤ π,
а так как котангенс
угла π/2 – α равен х,
то имеем:
arcсtg x = π/2 – α.
Складывая равенства
arctg x = α,
arcctg x = π/2 – α ,
получим:
arctg x + arcctg x = π/2,
ПРИМЕРЫ:
sin
(arcsin 1/2) = 1/2.
sin (arcsin 1) = 1.
ПРИМЕР:
Нельзя писать
sin (arcsin 1,2) = 1,2,
ПРИМЕР:
ПРИМЕР:
ПРИМЕР:
ПРИМЕР:
Найти
arcsin (sin
2).
РЕШЕНИЕ:
Требуется найти угол, лежащий в пределах от – π/2 < до < π/2, синус которого равен sin 2. Заметим, что если угол х
удовлетворяет неравенствам
– π/2 ≤ х ≤ + π/2,
то равенство
arcsin (sin х) = х справедливо. В противном же
случае последнее равенство не имеет места. В нашем же случае
π/2 < 2 < π.
Применив формулу приведения получим
sin 2 = sin (π – 2).
Теперь уже угол π –
2
удовлетворяет неравенствам
– π/2 < π – 2 ≤ π/2,
и поэтому можно писать:
arcsin [sin (π – 2)] = π – 2.
Следовательно,
arcsin (sin
2) = π – 2.
ПРИМЕР:
Вычислить:
arcsin (sin 8π/7).
РЕШЕНИЕ:
Число 8π/7 не принадлежит отрезку [–π/2; π/2].
Поэтому заменим sin 8π/7 синусом числа из отрезка [–π/2; π/2].
Так как
sin 8π/7 = sin (π + π/7) =
– sin π/7 = sin (–π/7) то
ПРИМЕР:
Вычислить:
arccos (cos 9π/8).
РЕШЕНИЕ:
Число 9π/8 не принадлежит отрезку [0; π].
Поэтому нужно найти на отрезке [0; π] такое число, косинус которого равен cos 9π/8.
Так как
cos (π + β) = cos (π – β), то
cos 9π/8 = 7π/8, где 0 ≤ 7π/8 ≤ π. Поэтому
arccos(cos 9π/8) = arccos(cos 7π/8) = 7π/8.
ПРИМЕР:
Вычислить:
arccos (cos 6).
РЕШЕНИЕ:
Так как 3π/2 < 6 < 2π, то
–2π < –6 < –3π/2 и
0 < 2π – 6 < π/2,
cos(2π – 6) = cos 6.
Поэтому
ПРИМЕР:
Вычислить:
arctg(tg 5π/8).
РЕШЕНИЕ:
Так как tg 5π/8 = – tg 3π/8 =
= tg (–3π/8) и
– π/2 < –3π/8 < π/2 то
ПРИМЕР:
Вычислить:
arcctg [ctg(–π/5)].
РЕШЕНИЕ:
Так как
сtg (–π/5) = –сtg π/5 = сtg 4π/5 и
0 < 4π/5 < π то
у = sin(2 arcsin х).
Обозначив arcsin х через α, будем иметь
sin 2α = 2 sin α cos α,
откуда
sin
(2 arcsin x) =
ПРИМЕР:
cos
(2 arccos x) =
=
cos2 (arccos x) – sin2
(arccos x) =
= x2 – (1 – x2) = 2x2 – 1.
ПРИМЕР:
соs (2 arcсоs 3/5) =
=
2(3/5)2 – 1 =
ПРИМЕР:
Найти значение выражения
arctg 1/3 + arctg 1/5 + arctg 1/7 + arctg 1/8.
РЕШЕНИЕ:
Учитывая, что
1/3 ∙ 1/5 < 1 и 1/7 ∙ 1/8 < 1,
ДРУГИЕ УРОКИ- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований





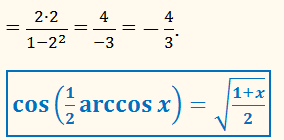

















Комментариев нет:
Отправить комментарий