понедельник, 16 мая 2022 г.

Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований

ВИДЕО УРОК

Общий вид преобразования функции.

Преобразования графиков функций – это линейные преобразования функции  y = f(x)  или её аргумента  х  к виду

y = af(kx + b) + m,

а так же преобразование с использованием модуля.

Зная, как строить графики функции  y = f(x), где

y = sin x, 

y = cos x,

y = tg x,

y = ctg x,

можно построить график функции

y = af(kx + b) + m.

Преобразование графиков тригонометрических функций подчиняется общей схеме геометрических преобразований

±k1× f(±k2× (x + a)) + b.

Но надо обратить внимание на влияние коэффициента  k2  на период тригонометрических функций. При отличном от единицы коэффициенте  k2  период становится равным
То есть, при  0 < k2 < 1  растяжение графика функции вдоль оси абсцисс соответствует увеличению периода, а при  k2 ˃ 1 сжатие графика соответствует уменьшению периода. Коэффициент  k1  влияет на амплитуду колебаний синусоиды и косинусоиды.

Параллельный перенос графика вдоль оси абсцисс на  |b|  единиц.

y = f(x – b)

вправо, если  b ˃ 0;

влево, если  b < 0.

y = f(x + b)

влево, если  b ˃ 0;

вправо, если  b < 0.

ПРИМЕР:

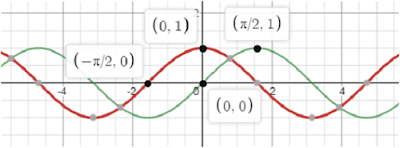
Построить график функции

y = sin (x + π/2),

пользуясь графиком

y = sin x

РЕШЕНИЕ:

Построим график функции

y = sin x
Сдвинем влево график функции

y = sin x

на  π/2.
Получим график функции (красная линия)

y = sin (x + π/2)

Параллельный перенос графика вдоль оси ординат на  |m|  единиц.

y = f(x) + m

вверх, если  m ˃ 0;

вниз, если  m < 0.

Отражение графика.

y = f(–x)

Симметричное отражение графика относительно оси ординат.

Сжатие и растяжение графика.

Здесь речь идет о построении графиков функций вида:

y = m sin kx,

y = m cos kx,

y = m tg kx,

y = m ctg kx.

y = f(kx)

При  k ˃ 1 – сжатие графика к оси ординат в  k  раз,

при  0 < k < 1 – растяжение графика от оси ординат в  k  раз,

Вообще говоря, построение графика функции

y = m sin kx

осуществляется в три этапа:

1. Строят график функции  y = sin x.

2. Строят график функции  y = sin kx.

3. Строят график функции  y = m sin kx.

Аналогично обстоит дело с другими тригонометрическими функциями.

На практике обычно при построении графика функции

y = m sin kx (y = m соs kx)

выполняют растяжение и сжатие для одной полуволны графика функции

y = sin x (y = соs x),

а затем строят весь график.

При построении графика функции

y = m tg kx (y = m сtg kx)

выполняются растяжение и сжатие для одной ветви графика функции

y = tg x (y = сtg x),

а затем строят весь график.

ПРИМЕР:

Построить график функции:

y = –3 соs 2x.

РЕШЕНИЕ:

Построим одну полуволну графика функции

y = соs x.

Осуществив её сжатие к оси  у  с коэффициентом  2, получим график функции

y = соs 2x.

Теперь осуществим растяжение полученного графика от оси  х  с коэффициентом  3, а затем преобразования симметрии относительно оси  х. В результате мы получим график функции

y = –3 соs 2x.

На рисунке
показана одна полуволна графика, а на рисунке
весь график.

Преобразования графика с модулем.

у = | f(x)|

При  f(x) ˃ 0 – график остаётся без изменений,

при  f(x) < 0 – график симметрично отражается относительно оси абсцисс.

График гармонических колебаний  у = А sin (ωx + α).

Тригонометрические функции используются для описания колебательных процессов. Один из наиболее важных процессов такого рода описывается формулой

у = А sin (ωx + α).

Эту формулу называют формулой гармонических или синусоидальных колебаний. Величину  А  называют амплитудой колебания, она характеризует размах колебания. Величину  ω  называют частотой колебания. Чем больше  ω, тем больше число колебаний за единицу времени (число колебаний за единицу времени равно  ω/2π).

Наконец  α  называют начальной фазой колебания.

Если, например, груз, висящий на пружине, вывести из положения равновесия, то он начнёт совершать вертикальные колебания. Закон движения выражается формулой

у = А sin (ωx + α), где

у – отклонение груза от положения равновесия,

х – время.

Тот же закон встречается в теории переменного электрического тока. При вращении прямоугольной рамки, сделанной из проводящего электрический ток материала, в магнитном поле по ней идёт ток. Если рамка вращается равномерно, то сила тока меняется по закону гармонических колебаний

у = А sin (ωx + α).

Построим график функции

у = А sin (ωx + α).

Прежде всего преобразуем функцию к виду

у = А sin (ω(x + α/ω)).

Построение графика этой функции выполним в несколько этапов.

1. Осуществим параллельный перенос системы координат, поместив начало новой системы  х'у'  в точку  О' (–α/ω; 0).

2. В системе  х'у'  построим график функции

у' = sin x'

(при этом можно ограничиться одной полуволной).

3. Осуществив сжатие построенного графика к оси  у'  с коэффициентом  ω, получим график

у' = sin ωx'.

4. Осуществив растяжение последнего графика от оси  x'  с коэффициентом  А, получим требуемый график.

ПРИМЕР:

Построить график функции

у = 2 sin (х/3 – π/6).

РЕШЕНИЕ:

Имеем:

у = 2 sin (1/3 (х – π/2)).

Построение графика выполним в несколько этапов.

1. Осуществим параллельный перенос системы координат, выбрав началом новой системы точку

О' (π/2; 0).

В системе х'у'   нам нужно построить график функции

у' = 2 sin 1/3 x'.

2. Строим график функции

у' = sin x'.

3. Выполнив сжатие графика к оси  у'  с коэффициентом  1/3  (то есть растяжение с коэффициентом  3), получим график функции

у' = sin х'/3.

4. Осуществим растяжение последнего графика от оси  у'  с коэффициентом  2.

Полученный график является графиком функции

у = 2 sin (х/3 – π/6).
На практике вместо сжатия, растяжения и параллельного переноса часто поступают иначе. Отыскивают значения  х, при которых заданная функция обращается в нуль, и значения, при которых она принимает наибольшее и наименьшее значения. Далее график строят по точкам.

ПРИМЕР:

Построить график функции

у = 3 sin (2х + π/3).

РЕШЕНИЕ:

Решим сначала уравнение

3 sin (2х + π/3) = 0.

Имеем

2х + π/3 = πk,

x = – π/6 + πk/2, k ∈ Z.

Дадим параметру  k  два значения: 0  и  1.

При  k = 0  имеем х = – π/6.

При  k = 1  имеем  х = π/3.

Значит точки

А1(– π/6; 0)  и  А2(π/3; 0)

служат концами одной полуволны искомой синусоиды.

Далее, серединой отрезка  [– π/6;  π/3]  является точка  π/12, в которой функция

у = 3 sin (2х + π/3)

принимает максимальное значение, равное трём. Значит

M (π/12; 3) – точка максимума.

Отмечаем на координатной плоскости точки

А1(– π/6; 0), А2(π/3; 0)  и  M (π/12; 3)

и строим полуволну искомого графика.
После этого строим график заданной функции.
Задания к уроку 31

ДРУГИЕ УРОКИ

Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)