ВІДЕО УРОК
1. Нехай кут А – гострий.З геометрії відомо, що
квадрат стороні трикутника, що лежить проти гострого кута,
дорівнює сумі квадратів двох інших сторін без подвоєного добутку однієї з цих
сторін на відрізок її від вершини гострого кута до висоти.
Нехай
ВD ⊥
АС, АD = m.
Тоді
a2 = b2
+ с2 – 2bm.
З прямокутного трикутника АВD знаходимо:
m
= с cos A.
Підставляємо у попередню рівність замість m рівне йому вираз с cos A,
отримаємо наступну рівність:
a2
= b2 + с2 – 2bс cos A.
Виведемо теорему
косинусів, коли сторона трикутника лежить проти гострого кута, другим способом.
bc
= b cos α.
Остаточно маємо:
a2
= b2 + с2 – 2bс cos α,
що й треба було
довести.
a2 = b2
+ с2 + 2bm.
Але
m = с
cos ∠ DАВ,
і оскільки ∠ DАВ
– суміжний із кутом А
даного трикутника, то
∠ DАВ
= 180° – А.
Отже,
cos ∠ DАВ = cos (180° – А) = – cos А.
Тепер рівність
m = с
cos ∠ DАВ
набуде вигляду
m = –
с cos А.
Підставляємо отриманий вираз для m у рівність
a2 = b2
+ с2 + 2bm,
будемо мати:
a2 = b2
+ с2 + 2b(–с
cos А),
або
a2 = b2
+ с2 – 2bс cos А.
Виведемо теорему косинусів, коли сторона трикутника
лежить проти тупого кута, другим способом.
bc
= b cos (180°
– α) = – b cos.
Остаточно дістанемо:
a2
= b2 + с2 – 2bс cos α.
Теорему доведено.
a2 = b2
+ с2 – 2bс cos А = b2 + с2.
Але у прямокутному
трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів
a2 = b2
+ с2.
Порівнюючи
a2 = b2
+ с2 – 2bс cos А = b2 + с2
і
a2 = b2
+ с2,
a2 = b2
+ с2 – 2bс cos А.
НАСЛІДОК.
Якщо дві сторони одного трикутника відповідно дорівнюють двом
сторонам іншого трикутника, а кути, що лежать між цими сторонами, не рівні, то
проти більшого кута лежіть і більша сторона.
Формуладозволяє обчислити довжину однієї зі сторін трикутника за даними довжинами двох інших сторін та величиною кута, що лежить проти невідомої сторони.
Теорема косинусів може бути записана і для двох
інших сторін трикутника:
b2 = a2
+ с2 – 2aс cos B,
c2 = a2
+ b2 – 2ab cos C.
У
трикутнику АВС:
АС = 3, ВС = 5, АВ = 6.
Знайти
кут, що проти лежить стороні АВ.
РОЗВ'ЯЗАННЯ:
∠ АСВ = arccos (–1/15).
ВІДПОВІДЬ: arccos
(–1/15)
ЗАДАЧА:
Заданий
трикутник АВС, довжини сторін якого
АС = 17, ВС = 14,
∠ АСВ = 60°.
Знайти
довжину третьої сторони трикутника, що розглядається.
РОЗВ'ЯЗАННЯ:
Відповідно
до теореми косінусів
АВ2
= АС2 + ВС2
– 2 ∙ АС ∙
ВС
∙ cos ∠ АСВ =
= 172 + 142
– 2 ∙ 17 ∙
14
∙ cos 60° =
= 280 + 196 – 238 = 247.
Тоді
АВ
= √͞͞͞͞͞247.
ВІДПОВІДЬ: √͞͞͞͞͞247
ЗАДАЧА:
Одна
зі сторін трикутника більша за іншу на 8 см, а кут між ними дорівнює 120°. Знайдіть
периметр трикутника, якщо довжина третьої сторони дорівнює 28
см.
РОЗВ'ЯЗАННЯ:
Позначимо
одну із сторін трикутника як х, тоді величина іншої сторони дорівнює (х + 8) см.
Виходячи
з теореми косинусів, отримаємо:
282 = х2
+ (х + 8)2 – 2х(х
+ 8)cos 120°,
784 = х2
+ х2 + 16х + 64 – 2х(х + 8)(–0,5),
784 = 2х2
+ 16х + 64 + х(х + 8),
720 = 3х2
+ 16х + 8х,
3х2
+ 24х – 720 = 0
Таким
чином, периметр трикутника дорівнює:
Р = 12 + (12 + 8) + 28
= 60 (см).
ВІДПОВІДЬ: 60 см
ЗАДАЧА:
У
трикутнику АВС
сторона АС дорівнює 7√͞͞͞͞͞3 см, сторона
ВС дорівнює 1
см. Кут
С дорівнює 150°.
Знайдіть довжину сторони АВ.
РОЗВ'ЯЗАННЯ:
Застосуємо
теорему косинусів та відповідну формулу:
АВ2 = АС2 + ВС2
– 2∙АС∙ВС ∙ cos С.
АВ2
= (7√͞͞͞͞͞3)2
+ 12 – 2(7√͞͞͞͞͞3)cos
150°.
ЗАДАЧА:
У
трикутнику АВС сторона
ВС = 4 см,
сторона АС = 13 см.
Кут між ними дорівнює 60°.
Знайдіть невідому сторону АВ.
РОЗВ'ЯЗАННЯ:
Запишемо
для невідомої сторони АВ теорему
косинусів:
АВ2 = АС2 + ВС2
– 2∙АС∙ВС ∙ cos С.
Підставляючи відомі значення сторін та кута,
отримаємо:
АВ2
= 42 + 32 – 2∙4∙3 ∙ cos 60°,
АВ2
= 16 + 9 – 24 ∙ 1/2,
АВ2
= 13,
АВ
= √͞͞͞͞͞13.
ВІДПОВІДЬ: √͞͞͞͞͞13 см
ЗАДАЧА:
Сторони
трикутника дорівнюють відповідно 3, 7 і
8
см. Знайти кут, що лежить проти сторони довжиною 7
см.
РОЗВ'ЯЗАННЯ:
Позначимо сторони трикутника:
АВ = 3, ВС = 7, АС = 8,
ЗАДАЧА:
РОЗВ'ЯЗАННЯ:
З трикутника АВС знайдемо cos В.З трикутника СВМ з теореми косинусів знайдемо СМ:
СМ2 = СВ2 + МВ2
– 2∙СВ∙МВ ∙ cos В,
СМ2 = 32 + 62
– 2∙3∙6∙1/3 = 33,
СМ = √͞͞͞͞͞33.
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 24. Формули перетворень суми тригонометричних функцій в добуток
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 30. Графіки зворотних тригонометричних функцій
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень











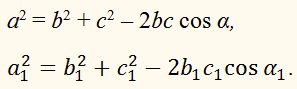

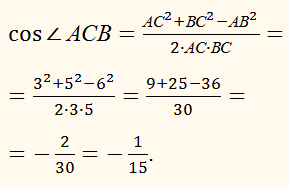









Комментариев нет:
Отправить комментарий