ВИДЕО УРОК
Формулы тригонометрии – это соотношения между основными тригонометрическими
функциями – синусом, косинусом, тангенсом и котангенсом.
Выражение, в котором переменная содержится под знаками
тригонометрических функций, называют тригонометрическим.
Основные тригонометрические тождества.
Из пяти основных тождеств вытекают три дополнительные.
Соотношения между тригонометрическими функциями одного и того же угла.
ОР = |х|, РМ = |у|,
а длина отрезка ОМ равна единице:
ОМ = 1.
Из прямоугольного треугольника ОРМ имеем:
ОР2 + РМ2 = ОМ2,
или
|х|2 + |у|2 = 1,
или
х2 + у2 = 1.
Но
х = sin α,
у = cos α,
а поэтому
sin2 α + cos2 α = 1.
х2 + у2 = 1,
а следовательно, и формула
sin2 α + cos2 α = 1
верны и в этом случае.
2. Из формул
х = cos α, у = sin α,
tg
α = у/х, сtg α = х/у
sin2 α + cos2 α = 1
sec2 α = 1 + tg2 α,
cosec2 α = 1 + ctg2 α.
Формула
sin2 α + cos2 α = 1
верна при всех
значениях α.
α = (2k + 1) π/2,
где k – любое целое число.
где k – любое целое число, так
как, если α = kπ, то функция ctg α и cosec α не определены (не существуют).
Наконец, формула
tg α ∙ ctg α = 1
верна при всех значениях α кроме тех, при которых не определена хотя бы
одна из функций tg α и ctg α, то есть при всех значениях α кроме
α = kπ/2,
где k – любое целое число.
Формулы
sec2 α = 1 + tg2 α,
cosec2 α = 1 + ctg2 α
sec α – гипотенуза прямоугольного треугольника с катетами 1 и tg α, а соsec α – гипотенуза
прямоугольного треугольника с катетами 1 и ctg α.
sin2 α + cos2 α = 1,
sec2 α = 1 + tg2 α,
cosec2 α = 1 + ctg2 α,
ПРИМЕР:
Упростите выражение:
(cos2 α
– 1)сtg2 α.
РЕШЕНИЕ:
ОТВЕТ:Формулы, которые выражают зависимость между тригонометрическими функциями одного и того же острого угла, представляют собой пример тригонометрических тождеств. Они справедливы независимо от величины угла.
Для доказательства тригонометрического тождества можно или левую часть тождества преобразовать к правой, или правую часть преобразовать к левой, или каждую из частей тождества преобразовать к одному и тому же выражению.
ПРИМЕР:
Доказать тождество:
tg2 α – sin2 α = tg2 α sin2 α.
ДОКАЗАТЕЛЬСТВО:
Первый
способ.
ПРИМЕР:
Доказать справедливость
тождества:
cos4 α – sin4 α = cos2 α (1 – tg α)(1 + tg α).
ДОКАЗАТЕЛЬСТВО:
Первый
способ.
Преобразуем правую часть:
cos2 α
(1 – tg α)( 1 + tg α) =
cos2 α
(1 – tg2 α) =
cos2 α
– sin2 α.
Второй
способ.
Преобразуем левую часть:
cos4 α – sin4 α =
(cos2 α – sin2 α)(cos2 α + sin2 α) =
cos2 α – sin2 α.
Правая и левая части данного
равенства преобразованы в одно и то же выражение
cos2 α – sin2 α.
ПРИМЕР:
Доказать тождество
3(sin4 α + cos4 α) – 2(sin6 α + cos6 α) = 1.
ДОКАЗАТЕЛЬСТВО:
Преобразуем вначале левую часть равенства, а затем, используя формулу
находим
3(sin4 α + cos4 α) – 2(sin6 α + cos6 α) =
ПРИМЕР:
Доказать тождество
sin3 α (1 + ctg α) + cos3 α (1 + tg α) = sin α + cos α.
ДОКАЗАТЕЛЬСТВО:
sin3 α (1 + ctg α) + cos3 α (1 + tg α) =
= sin2 α (sin α + cos α) + cos2 α (cos α + sin α)
ДРУГИЕ УРОКИ- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований





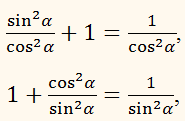




















Комментариев нет:
Отправить комментарий