Урок 2. Прямая призма

ВИДЕОУРОК

Многогранные углы.

Многогранным углом называется фигура, состоящая из нескольких лучей  ОА, ОВ, ОС, …, ОF, выходящих из одной точки  О  и не лежащих в одной плоскости, и из плоских углов  АОВ, ВОС,…, FОА  между этими лучами.

Общая точка  О  пересечения всех лучей называется вершиной многогранного угла, лучи  ОА, ОВ, ОС, …, ОF – его ребрами, части плоскостей, заключенные между ребрами, называются его гранями, а углы  АОВ, ВОС,…, FОА, образованные ребрами, лежащими в одной грани, называются плоскими углами многогранного угла.

Многогранный угол называется выпуклым, если он целиком лежит по одну сторону от плоскости, совпадающей с любой его гранью.

Два многогранных угла считаются равными, если они при наложении совпадают всеми своими частями.

Сумма плоских углов выпуклого многогранного угла меньше  360°.

Трёхгранные углы.

Если число граней многогранного угла равно трём, то его называют трёхгранным углом.

Основные свойства трёхгранных углов:

– сумма двух плоских углов трёхгранного угла больше третьего его плоского угла;

– каждый плоский угол трёхгранного угла меньше разности двух других его плоских углов.

Равными трёхгранными углами называются такие углы, которые при наложении совмещаются во всех своих частях.

Следовательно, у равных трёхгранных углов все двугранные и плоские углы соответственно равны между собой, но обратное утверждение несправедливо. Существуют такие трёхгранные углы, у которых двугранные и плоские углы соответственно равны, а трёхгранные углы не равны между собой.

ПРИМЕР:

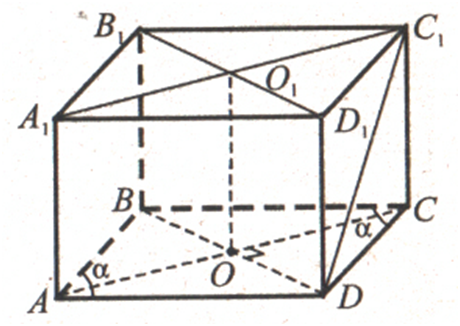
На рисунке изображены два трёхгранных угла, у которых плоские і двугранные углы соответственно равны, а совместить эти углы невозможно.

Трёхгранные углы невозможно совместить, из-за неодинаковой ориентации их соответственных граней относительно вершины. Грани  АОВ, ВОС  и  СОА  ориентированы относительно вершины  О  против движения часовой стрелки, а соответствующие грани  

А₁ОВ₁, В₁ОС₁  и  С₁ОА₁ – ориентированы по движению часовой стрелки, и трёхгранные углы  

ОАВС  и  ОА₁В₁С₁ не равны, хотя в них равны и все плоские, и все двугранные углы.

Таким образом, для равенства двух трёхгранных углов с соответственно равными плоскими и двугранными углами необходимо ещё, чтобы их грани были одинаково ориентированы относительно их вершин.

Признаки равенства трёхгранных углов.

Существуют признаки равенства трёхгранных углов, аналогичные признакам равенства треугольников в планиметрии.

– если два одинаково ориентированных трёхгранных угла имеют по равному плоскому углу, прилежащему к двум соответственно равным двугранным углам, то такие трёхгранные углы равны;

– если два одинаково ориентированных трёхгранных угла имеют по два равных плоских угла, плоскости которых образуют равные двугранные углы, то такие трёхгранные углы равны;

–  если два одинаково ориентированных трёхгранных угла имеют по три соответственно равных плоских угла, то такие трёхгранные углы равны;

– если два трёхгранных угла одинаково ориентированы и имеют по три соответственно равных двугранных угла, то такие трёхгранные углы равны.

Основные определения.

Многогранником называется геометрическое тело, поверхность которого состоит из частей плоскостей, ограниченных многоугольниками.

Гранями многогранника называются части плоскостей (многоугольники), ограничивающие многогранник.

Ребрами многогранника называются общие стороны смежных граней (многоугольников).

Вершинами многогранника называются вершины многогранных углов, образованных его гранями, сходящимися в одной точке.

Диагональю многогранника называется отрезок прямой, соединяющей две вершины многогранника, не лежащие в одной грани.

Диагональной плоскостью многогранника называется плоскость, проходящая через три вершины многогранника, не лежащие в одной грани.

Сечением многогранника плоскостью называется часть этой плоскости, ограниченная линией пересечения поверхности многогранника с этой плоскостью.

Многогранник называется выпуклым, если он целиком лежит по одну сторону от плоскости любой его грани.

Гранями выпуклого многогранника могут быть только выпуклые многоугольники.

Для каждого выпуклого многогранника

Сумма числа вершин  В  и числа граней  Г  на  2  больше числа его рёбер  Р:

В + Г – Р = 2.

Призма.

Призмою называется многогранник, две грани которого параллельны, а остальные пересекаются по параллельным прямым.

Грань, на которой <<стоит>> призма, да противоположная ей грань называются основами призмы, а все другие – боковыми гранями.

Из определения призмы следует, что в основаниях призмы лежат равные многоугольники с соответственно параллельными сторонами, а боковые грани призмы – параллелограммы.

Общие стороны боковых граней призмы называются боковыми ребрами призмы.

Отрезок  ОО₁ прямой, перпендикулярный плоскостям оснований призмы, и заключённый между ними, называется высотой призмы.

Диагональной плоскостью призмы принято называть плоскость, проходящую через диагональ основания и боковое ребро призмы, а фигуру  Е₁С₁СЕ, полученную при пересечении этой плоскости с поверхностью призмы, называют диагональным сечением призмы.

Сечение призмы плоскостью, перпендикулярной её боковым ребрам, называют перпендикулярным сечением призмы. Диагональное сечение призмы – параллелограмм.

На рисунке фигура  A₂B₂C₂D₂E₂  является перпендикулярным сечением призмы.

n-угольная призма имеет  2n  вершин, n + 2  граней, 3n  ребер.

Прямая призма.

Призма называется прямой, если её боковые ребра перпендикулярны к плоскости основания.

В прямой призме высота  ОО₁  параллельна всем её боковым рёбрам  АА₁, ВВ₁, СС₁… .

Все боковые ребра прямой призмы равны между собой. Каждое из них будет высотой прямой призмы. Все боковые грани – прямоугольники.

Прямая призма называется

и т. д. в зависимости от того, какой многоугольник лежит в её основании.

Поверхность прямой призмы.

Боковою поверхностью прямой призмы называется сумма площадей всех её боковых граней.

Полной поверхностью прямой призмы называется сумма её площади боковой поверхности и площадей оснований.

Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы.

Рассмотрим прямую треугольную призму и её развёртку.

Пусть длины сторон треугольника, который находится в основании призмы, равны

ВС = а, АС = b, АВ = с,

а длина боковых рёбер

АА₁, ВВ₁, СС₁ – H.

Тогда площадь боковой поверхности этой призмы будет:

S_б = аH + bH + сH =

(а + b + с)H = РH,

где  Р – периметр треугольника, который лежит в основании.

ЗАДАЧА:

По данной на рисунку развёртки прямой треугольной призмы (размеры даны в сантиметрах) найдите площадь её боковой и полной поверхности.

Площадь боковой поверхности призмы находим по формуле

S_б = PH,

где  P = 5 + 8 + 5 = 18 (cм),

Н = 12 см,

S_б =18 × 12 = 216 (см)²

Площадь полной поверхности призмы равна сумме площади боковой поверхности и площади двух треугольников, которые являются основаниями.

где  a = 8 cм, h = 3 cм.

Выполним вычисления:

Поэтому,

S_п = 216 + 12 × 2 = 240 (см)².

Решение стереометрических задач с помощью тригонометрии.

ЗАДАЧА:

Основанием прямой призмы – ромб с тупым углом  150°. Площадь боковой поверхности призмы равна  96 см², а площадь её полной поверхности – 132 см². Найдите высоту призмы.

РЕШЕНИЕ:

Пусть ABCDA₁B₁C₁D₁ – прямая призма, 
ABCD – ромб,

∠ ADC = 150°, 
S_б = 96 см², 
S_п = 132 см².

S_п – S_б = 2S_ABCD 
= 132 – 96 = 36 (см²),

откуда  S_ABCD = 18 (см²).

Поэтому,

S_ABCD = AD² × sin ∠ ADC.

Откуда

ОТВЕТ:  4 см.

ЗАДАЧА:

Основание прямой призмы – ромб с острым углом  α. Диагональное сечение призмы, проходящее через большую диагональ основания, имеет площадь  S. Найдите площадь боковой поверхности призмы.

РЕШЕНИЕ:

Пусть  АВСDА₁В₁С₁D₁ – заданная призма.

АВСD – ромб, ∠ С = ∠ А = ∠ α – острый. Тогда  АС – большая диагональ ромба. AА₁C₁C – заданное диагональное сечение и

Пусть сторона ромба равна  а. По свойству диагоналей ромба  ∠ ACD = ^α/₂. DO ⊥ (OCC₁), поскольку  OD ⊥ OC  и  OD ⊥ OO₁. Аналогично  D₁O₁ ⊥ (O₁C₁C). Таким образом, проекцией грани  DD₁C₁C  на заданное диагональное сечение является четырехугольник  OO₁C₁C. (площадь которого равна  ^S/₂). Угол между этими плоскостями равен  ^α/₂

 (DC ⊥ CC₁, OC ⊥ CC₁, ∠ DCO = ^α/₂). Поэтому

ОТВЕТ:

ЗАДАЧА:

Основание прямой призмы – ромб с острым углом  α, площадь которого равна  S. В призме проведено диагональное сечение, проходящее через меньшую диагональ основания. Диагональ этого сечения наклонена к плоскости основания под углом  β. Найдите площадь боковой поверхности призмы.

РЕШЕНИЕ:

Пусть  ABCDA₁B₁C₁D₁ – заданная призма.

АВСD – ромб,

∠ С = ∠ А = ∠ α – острый. Тогда  ВD – меньшая диагональ ромба.

BDD₁C₁ – диагональное сечение. Отрезок  BD – проекция диагонали  B₁D   на плоскость основания. Поэтому  ∠ B₁DВ – угол наклона диагонали  B₁D  к плоскости основания. По условию,

∠ B₁DВ = β,

S_ABCD = DC² sin ∠ С.

Одержимо:

S = DC² sin ∠ α,

Из  ∆ COD (∠ O = 90°):

S_б = P∙ H = 4DC ∙ BB₁ =

ОТВЕТ:

Задания к уроку 2

• Задание 1
• Задание 2
• Задание 3

Другие уроки:

• Урок 1. Прямые и плоскости в пространстве
• Урок 3. Наклонная призма
• Урок 4. Правильная призма
• Урок 5. Параллелепипед
• Урок 6. Прямругольный параллелепипед
• Урок 7. Куб
• Урок 8. Пирамида
• Урок 9. Правильная пирамида
• Урок 10. Усечённая пирамида
• Урок 11. Цилиндр
• Урок 12. Вписанная и описанная призмы
• Урок 13. Конус
• Урок 14. Усечённый конус
• Урок 15. Вписанная и описанная пирамиды
• Урок 16. Сфера и шар
• Урок 17. Комбинация тел