Уроки математики и физики (RU + UA)

▼

пятница, 5 сентября 2014 г.

Урок 17. Множення звичайних дробів

ВИДЕО УРОК

Тут багато доведеться робити по-новому, тому що дія множення дробів багато в чому відрізняється від множення над натуральними числами.

Множення звичайного дробу на звичайний дріб.

Добутком дробів називають таку дріб, чисельник якого дорівнює добутку числівників даних дробів, а знаменник - добутку їх знаменників.

Щоб помножити дріб на дріб, потрібно помножити чисельник на чисельник, а знаменник на знаменник і перший добуток зробити чисельником, а друге – знаменником добутку.
При множенні слід робити (якщо можливо) скорочення.

 ПРИКЛАД:
Наведемо приклад, який ілюструє правило множення звичайних дробів.

ПРИКЛАД:

 Розглянемо квадрат зі стороною  1 од., При цьому його площа дорівнює  1 ед2.
Розділимо цей квадрат на рівні прямокутники зі сторонами  1/4 од. і   1/8 од., при цьому вихідний квадрат буде складатися з

4 ∙ 8 = 32

 прямокутників. Отже, площа кожного прямокутника становить  1/32  частку площі вихідного квадрата, тобто вона дорівнює  1/32  од2. Тепер закрасимо частина вихідного квадрата.
Сторони закрашеного прямокутника рівні  5/8 од. і  3/4 од., значить, його площа дорівнює добутку дробів  5/8  і  3/4, тобто,
Але зафарбований прямокутник складається з 15 маленьких прямокутників, значить його площа дорівнює  15/32 од2.
Отже,
Так як

 5 ∙ 3 = 15
8 ∙ 4 = 32,

то остання рівність можна переписати як
що підтверджує формулу множення звичайних дробів.
З допомогу цього правила множення можна множити і правильні і неправильні дроби, і дроби з однаковими знаменниками, і дроби з різними знаменниками.

ПРИКЛАД:

Виконайте множення звичайного дробу  7/11  на звичайну дріб  9/8.

РОЗВ'ЯЗАННЯ:

Добуток чисельників дробів  7  і  9  дорівнює 63, а добуток знаменників  11  і  8  одно  88. Таким чином, множення звичайних дробів  7/11  і  9/8  дає дріб  63/88.
Короткий запис вирішення:
ВІДПОВІДЬ:  63/88

Пам'ятайте про скорочення отриманої дробу, якщо в результаті множення виходить скоротна дріб, і при виділенні цілої частини з неправильного дробу.

ПРИКЛАД:

Виконайте множення звичайного дробу  4/15  на звичайну дріб  55/6.

РОЗВ'ЯЗАННЯ:

 Застосуємо правило множення звичайних дробів:
Очевидно, що отримана дріб скоротливості. Виконаємо скорочення дробу. 

НОД (220; 90) = 10.
Залишилося виділити цілу частину з отриманої неправильного дробу:
Короткий запис вирішення:
ВІДПОВІДЬ:  24/9

 Скорочення дробу можна проводити до обчислення добутків 
чисельників і добутків знаменників дробів, тобто коли дріб має вигляд
Для цього числа

a, b, c, d

замінюють їх розкладаннями на прості множники, після чого скорочуються однакові множники чисельника і знаменника.
Вирішимо попередній приклад іншим способом.

ПРИКЛАД:

Виконайте множення звичайного дробу  4/15  на звичайну дріб  55/6.

РОЗВ'ЯЗАННЯ:

 Застосуємо правило множення звичайних дробів:
Так як

4 = 2 ∙ 2,
55 = 11 ∙ 5,
15 = 5 ∙ 3,
6 = 2 ∙ 3, то
Тепер скорочуємо загальні прості множники:
Обчислимо твори в чисельнику і знаменнику дробу, після чого виділимо цілу частину з неправильного дробу.
Короткий запис вирішення:
ВІДПОВІДЬ:  24/9

 Для множення дробів характерно переместітельная властивість, тобто дроби можна міняти місцями при множенні:
Множення звичайного дробу на натуральне число.

Сенс множення звичайного дробу на натуральне число з'ясовується з наступного визначення: помножити звичайну дріб (множимое) на натуральне число (множник) – значить знайти цю дріб множимо.

Щоб помножити натуральне число на дріб, треба помножити 
натуральне число на чисельник дробу і цей добуток зробити чисельником, а знаменником підписати знаменник даної дробу.

За допомогою букв правило множення дробу  a/b  на натуральне число n  має вигляд:
Ця формула випливає з формули множення двох звичайних дробів:
Представивши натуральне число як дріб зі знаменником 1, отримаємо:
Якщо врахувати, що ціле число являє собою дріб зі знаменником 1, то множення дробу на ціле число і цілого числа на дріб можна виконати за цим же правилом.

ПРИКЛАД:
ПРИКЛАД:
ПРИКЛАД:

Виконайте множення дробу  2/27  на  5.

РОЗВ'ЯЗАННЯ:

 Множення чисельника  2  на число  5  дає  10, тому в силу правила множення дробу на натуральне число, lj,enjr  2/27  на  5  дорівнює дробу  10/27.
ВІДПОВІДЬ:  10/27 

При множенні дробу на натуральне число отриману дріб часто доводиться скорочувати, а якщо вона ще й неправильна, то уявити її у вигляді змішаної дробу.

ПРИКЛАД:

Виконайте множення дробу  5/12  на  8.

РОЗВ'ЯЗАННЯ:

 За формулою множення дробу на натуральне число маємо:
Отримана дріб скоротливості. Виконаємо скорочення дробу. Так як

 НОК (40: 12) = 4, то
Залишилося виділити цілу частину:
Короткий рішення прикладу:
Скорочення можна було провести, замінивши числа в чисельнику і знаменнику їх розкладанням на прості множники. У цьому випадку рішення виглядало б так:
ВІДПОВІДЬ:  31/3

 Множення дробу на натуральне число має переместітельним властивістю, тобто добуток дробу на натуральне число, дорівнює добутку цього натурального числа на дріб.
Множення змішаних чисел.

Щоб перемножити мішані числа, потрібно попередньо звернути їх у неправильні дроби і потім перемножити за правилом множення дробу на дріб.

ПРИКЛАД:
Якщо ж перемножують змішане число на ціле, то простіше множити окремо цілу і дробову частини.

 ПРИКЛАД:
Закони та правила множення натуральних чисел справедливі і для дробів. Їх використання спрощує усні і письмові обчислення.
Добуток дрібних чисел підпорядковується переместительному, сочетательному і розподільному закону.
Якщо один з співмножників – ціле число, то множення може бути виконано на підставі розподільного закону.               

ПРИКЛАД:

42/5 × 3 = (4 + 2/5) × 3
= 4 × 3 + 2/5  × 3
= 12 + 6/5 = 131/5. 

ПРИКЛАД:    

97/8 × 8 = 9 × 8 + 7/8 × 8
= 72 + 7 = 79.

Якщо один з двох співмножників збільшимо в кілька разів, а інший залишимо без зміни, то добуток збільшиться в стільки ж разів.
Якщо один з співмножників зменшимо в кілька разів, а інший залишимо без зміни, то добуток зменшиться в стільки ж разів.

Множення трьох і більшої кількості дробів.

Властивості множення натуральних чисел поширюються і на множення дробів.
І сполучна властивості множення дозволяють однозначно визначити множення трьох і більшої кількості дробів. При цьому все відбувається за аналогією з множенням трьох і більшої кількості натуральних чисел. Зокрема, дробу і натуральні числа в добутку можна для зручності обчислення переставляти місцями, а при відсутності дужок, що вказують порядок виконання дій, можна самим розставити дужки будь-яким з доступних способів.

ПРИКЛАД:    

3/4 × (79/31 × 11/3) =
(3/4 × 4/3) × 79/31 =
1 × 79/31 = 79/31.

ПРИКЛАД:    

(122/5 × 435/17) × 5/31 =
(122/5 × 5/31) × 435/17
= 2 × 435/17 = 8610/17.

ПРИКЛАД:

Виконайте множення чотирьох звичайних дробів:   

1/20, 12/5, 3/7, 5/8.

РОЗВ'ЯЗАННЯ:

 Запишемо добуток, який нам потрібно обчислити:
В силу правила множення дробів записаний добуток дорівнює дробу, числівник якого дорівнює добутку числівників всіх дробів, а знаменник – добутку знаменників.
Перш ніж обчислити добутки в чисельнику і знаменнику, доцільно замінити всі множники їх розкладаннями на прості множники і провести скорочення:
ВІДПОВІДЬ:  9/280

ПРИКЛАД:

Виконайте множення п'яти чисел:
РОЗВ'ЯЗАННЯ:

 У цьому творі зручно згрупувати дріб  7/8  з числом  8, а число  12  з дробом  5/36, це дозволить спростити обчислення, так як при такому угрупованні очевидно скорочення. Маємо
ОТВЕТ:  116 2/3

Завдання до уроку 17
Інші уроки:
на

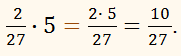
Комментариев нет:

Отправить комментарий