ВИДЕО УРОК
ПРИКЛАД:
Якщо
число 5
треба помножити на 7,
то пишуть
5 × 7 = 35
І
кажуть, що треба знайти суму семи однакових доданків.
5 + 5 + 5 + 5 + 5 + 5 + 5
= 5 × 7.
= 5 × 7.
Множенням називається
дія, яка полягає в знаходженні суми однакових доданків.
Число, що є доданком, називається множеним;
число, яке показує, скільки таких однакових доданків, називається множником.
Результат діє, тобто число, знайдене при множенні, називається добутком.
Множене і множник іноді називають одним словом співмножники. Так,у
нашому прикладі 5 – множене, 7 – множник, 35
– добуток. Знак множення × ставиться між множеним і множником. Як знак
множення часто вживається крапка ∙ .
ПРИКЛАД:
3 × 5 = 15.
Перед буквеними співмножниками знак множення не
ставлять.
Якщо замість цифр при множенні пишуть букви, то знак
множення можна не ставити:
Якщо множене дорівнює одиниці, то добуток дорівнює
множникові.
Якщо множник дорівнює одиниці, то добуток
приймається рівним множеному.
ПРИКЛАД:
1 × 5 = 5,
10 × 1 = 10.
Якщо множене дорівнює нулеві, то добуток
дорівнює нулеві.
Якщо множник дорівнює нулеві, то добуток приймається
рівним нулеві.
ПРИКЛАД:
0 × 342 = 0,
37 × 0 = 0,
0 × 0 = 0.
Ці властивості можна записати за допомогою змінної.
При будь-яких значеннях b правильні рівності:
1
×
b = b,
0 × b
= 0.
ЗАКОНИ
МНОЖЕННЯ
Переставний
закон.
При множенні чисел ми можемо співмножники міняти м'ясницями.
У цьому і полягає переставний закон множення, який можна сформулювати так:
Добуток не змінюється
від зміни місць співмножників.
Переставний закон можна виразити коротко за
допомогою букв. Якщо позначити перший співмножник буквою a,
а другий – буквою b, то переставний закон
можна записати у вигляді такої рівності:
Якщо співмножників більше як два, наприклад три, то переставний закон
залишається в силі:Сполучний закон.
Добуток не зміниться,
якщо яку-небудь групу співмножників, що стоять поряд, ми замінимо їх добутком.
Цей закон називається сполучним. Його назва повинна нагадувати
нам про те, що при множенні кількох чисел співмножники можна об'єднувати
(сполучати) в групи. У загальному вигляді цей закон можна записати так:
Добуток суми кількох
чисел на яке-небудь число дорівнює сумі добутків кожного доданка на це число.
Запишемо його в загальному вигляді для випадку трьох
доданків:
Згідно з цим законом: множення, розподілити між
окремими доданками. Оскільки добуток не змінюється від переставлення
співмножників, то з розподільного закону випливає, що множення числа на суму
можна замінити множенням цього числа на кожний доданок окремо з дальшим
додаванням результатів, тобто:Множення добутку на число і числа на добуток.
Щоб помножити добуток кількох
чисел на будь-яке число (чи навпаки), досить один із співмножників добутку
помножити на це число, залишивши інші співмножники без зміни.
ПРИКЛАД:
(35 × 12) ×
4 =
(35 × 4) ×12
=
140 × 12 = 1680,
20 × (7 ×
18
×
5)
= (20 ×
5) ×
7 ×
18
=100 × 7 × 18 = 12600.
Множення
різниці на число.
Щоб помножити різницю
на число, досить помножити на це число окремо зменшуване і від'ємник і потім
від першого добутку відняти другий.
(35 – 15) ×
4 =
35 × 4 – 15 ×
4
=140 – 60 = 80.
Множення
многоцифрових чисел на письмі.
ПРИКЛАД:
236 × 4.
Ми
можемо подати 236 як суму трьох доданків
(200 + 30 + 6) і,
користуючись
розподільним законом, помножити окремо сотні, десятки і одиниці, на 4 і
знайдені добутки додати:
(200 + 30 + 6) × 4 =
200 × 4 + 30 × 4 + 6 × 4
= 800 + 120 + 24 = 944.
Проте такий запис множення займає
богато місця. Тому прийнято починати множення з нижчих розрядів, а проміжні
обчислення виконувати в думці.
ПРИКЛАД:
236 × 4 = 944.
При ціому треба міркувати так. Починаємо множення з одиниць і
говоримо:
4 × 6 = 24,
число 4 пишемо, а 2 десятки запам’ятовуємо,
щоб потім додати їх до добутку десятків; 3 десятки помножаємо
на 4, буде 12 десятків, та ще 2 – всього 14 десятків; 4 десятки пишемо, а 10 десятків, тобто
сотню, запам'ятовуємо, щоб потім додати до сотень; 2 сотні помножаємо
на 4, буде 8 сотень, та ше
1 сотня – всього 9 сотень.
ПРИКЛАД:
Помножимо 618 на 325.
Тут множник – трицифрове число. Тому
спочатку ми помножили множене на одиниці множника (618
× 5)
і дістали перший проміжний добуток 3090; потім помножили множене на десятки множника (618
× 2),
дістали другий проміжний добуток 1236 і почали підписувати його під десятками
першого; потім
помножили множене на сотні множника (618
× 3),
дістали третій проміжний добуток 1854 і почали підписувати його під сотнями перших.
Нарешті, ми додали три проміжні добутки і знайшли загальний добуток 200 850.
Помножимо 642
на 305.
Тут ми спинимося тільки на особливостях цього випадку. Число 305, що є множником, має нуль на місці десятків. На
цей нуль ми також помножали множене 642 і
дістали другий проміжний добуток, що дорівнює нулеві. Він позначений у
нас трьома нулями, бо ми міркували так:
642 × 0 = 0, бо
2 × 0 = 0;
4 × 0 = 0;
6 × 0 = 0.
З останнього прикладу ми зробимо висновки:
– проміжний добуток
треба починати підписувати під тією розрядною одиницею, на яку виконується
множення, наприклад, крайня права цифра
6 третього добутку написана під
сотнями, бо іє дістали від множення на сотні.
– нулі, поставлені на
місці другого проміжного добутку, писати не слід, але треба пам'ятати, що
крайня права цифра третього добутку повинна стояти під сотнями, а не під
десятками.
Щоб помножити
натуральне число на 10, 100, 1000, … , треба приписати до цього числа праворуч стільки
нулів, скільки їх у числі, на яке множимо.
ПРИКЛАД:
23 × 100 = 2300;
83 × 1000 = 83000.
Щоб помножити
натуральні числа, які закінчуються нулями, треба:
– виконати множення,
не звертаючи уваги на нулі в кінці чисел;
– до знайденого
добутку приписати праворуч стільки нулів, скільки їх у всіх множниках разом.
Щоб помножити число на
добуток кількох чисел, досить помножити його на перший співмножник, потім на
третій і т. д.
Щоб помножити добуток
на яке-небудь число, досить помножити на це число один із співмножників,
залишивши інші без змін.
Перевірка множення.
Множення можна перевірити множенням; для цього треба
переставити співмножники і знову їх перемножити.
СПОСОБИ
ШВИДКОГО МНОЖЕННЯ
Множення
на число, близьке до одиниці якось розряду.
ПРИКЛАД:
405 × 97 = 405(100 – 3)
= 405 ×
100 – 405 × 3 =
40500 – 1215 = 39285,
8012 ×
1006 =
8012(100 + 6) =
8012000 + 8012 ×
6 =
8012000 + 48072 = 8060072.
Множення 9, 99, 999.
Щоб помножити на число, написане
дев'ятками, треба до
множеного приписати справа стільки нулів, скільки
дев'яток у множнику, і від результату
відняти множене.
ПРИКЛАД:
378 × 9 = 3870 – 387
= 3483,
24 × 99 = 2400 – 24
= 2376,
18 × 999 = 18000 – 18
= 17982.
Множення двозначного числа на 11.
Щоб помножити двозначне число, сума цифр якого менша
за 10,
на 11,
треба між цифрами числа написати суму його цифр.
ПРИКЛАД:
72 × 11 = 792.
Щоб помножити на 11 двозначне
число, сума цифр якого більша або дорівнює 10, треба між цифрою
десятків,збільшеною на 1,і
цифрою одиниць написати надлишок суми цифр числа над 10.
ПРИКЛАД:
68 × 11 = 748.
Завдання до уроку 5
Інші уроки:
- Урок 1. Нумерація
- Урок 2. Додавання натуральних чисел
- Урок 3. Віднімання натуральних чисел
- Урок 4. Таблиця множення
- Урок 6. Ділення натуральних чисел
- Урок 7. Степінь числа
- Урок 8. Вимірювання величин
- Урок 9. Ділення с остачею
- Урок 10. Подільність натуральних чисел
- Урок 11. Найбільшій спільний дільник (НСД)
- Урок 12. Найменше спільне кратне (НСК)
- Урок 13. Звичайні дроби
- Урок 14. Перетворення дробів
- Урок 15. Додавання дробів
- Урок 16. Віднімання дробів
- Урок 17. Множення дробів
- Урок 18. Ділення дробів
- Урок 19. Знаходження дробу від числа (задачи)
- Урок 20. Знаходження числа за відомою його частиною (задачи)
- Урок 21. Кінечни десяткові дроби
- Урок 22. Додавання десяткових дробів
- Урок 23. Віднимання десяткових дробів
- Урок 24. Множення десяткових дробів
- Урок 25. Ділення десяткових дробів
- Урок 26. Округлення чисел





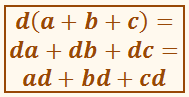


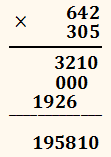
Комментариев нет:
Отправить комментарий