ВИДЕО УРОК
Віднімання дробів з однаковими знаменниками.
Спочатку наведемо приклад, який дозволить нам з'ясувати, як проводиться віднімання дробів з однаковими знаменниками.
ПРИКЛАД:
Нехай на тарілці знаходилося п'ять восьмих часток яблука, тобто, 5/8 яблука. Після чого дві восьмих частки забрали. За змістом віднімання, вказане дію можна записати так:
Зрозуміло, що при цьому на тарілці залишається
5 – 2 = 3 восьмих частки яблука, тобто
Розглянутий приклад ілюструє правило віднімання дробів з однаковими знаменниками.
Щоб відняти дріб з дробу з однаковими знаменниками, потрібно відняти чисельник від'ємника з чисельника зменшуваного і залишити колишній знаменник.
Озвучене в основному за рахунок букв записується так:
Цю формулу і будемо використовувати при відніманні дробів з однаковими знаменниками.
ПРИКЛАД:
Виконайте віднімання звичайного дробу 17/15 зі звичайної дроби
24/15.
РОЗВ'ЯЗАННЯ:
Знаменники віднімаються дробів рівні. Чисельник зменшуваного дорівнює 34, а чисельник від'ємника дорівнює 17, їх різниця дорівнює:
24 – 17 = 7.
Тому віднімання дробів з однаковими знаменниками 24/15 і 17/15 дає
дріб 7/15.
ВІДПОВІДЬ: 7/15
При можливості потрібно проводити скорочення дробу і (або) виділення цілої частини з неправильного дробу, яка виходить при відніманні дробів з однаковими знаменниками.
ПРИКЛАД:
Обчисліть різницю:
РОЗВ'ЯЗАННЯ:
Скористаємося формулою вирахування дробів з однаковими знаменниками.
Очевидно, що чисельник і знаменник отриманої дробу діляться на два, тобто дріб 22/12 – скоротна дріб. Виконавши скорочення цього дробу на 2, приходимо до дробу 11/6.
Дріб 11/6 неправильна, тому з неї потрібно виділити цілу частину.
Отже, що обчислюється різниця дробів з однаковими знаменниками дорівнює 15/6.
Короткий варіант рішення виглядає так:
ВІДПОВІДЬ: 15/6
ПРИКЛАД:
Віднімання дробів з різними знаменниками.
Віднімання дробів з різним и знаменниками зводиться до віднімання дробів з однаковими знаменниками. Для цього дробу з різними знаменниками досить привести до спільного знаменника.
Щоб відняти дріб з дробу з різними знаменниками, потрібно попередньо привести їх до найменшого спільного знаменника, потім з чисельника зменшуваного відняти чисельник від'ємника і під їх різницею підписати спільний знаменник.
ПРИКЛАД:
Відніміть від звичайного дробу 2/9 звичайну дріб 1/15.
РОЗВ'ЯЗАННЯ:
Так як знаменники віднімаються дробів різні, то спочатку виконаємо приведення дробів до найменшого спільного знаменника. Так як
НОК (9; 15) = 45,
то додатковим множником дробу 2/9 є число:
45 : 9 = 5,
а додатковим множником дробу 1/15 є число:
45 : 15 = 3,
тоді
Залишилося відняти від дробу 10/45 дріб 3/45, отримуємо
що і дає нам шукану різницю дробів з різними знаменниками.
Короткий рішення записується так:
ВІДПОВІДЬ: 7/45
Не слід забувати про скорочення отриманої після вирахування дробу, а також про виділення цілої частини.
ПРИКЛАД:
Відніміть з дробу 19/9 дріб 7/36.
РОЗВ'ЯЗАННЯ:
Після приведення дробів з різними знаменників до найменшого спільного знаменника 36, отримаємо дробу 76/36 і 7/36. Знаходимо їх різницю:
Отримана дріб скорочена, після її скорочення на 3, отримуємо 23/12. А ця дріб неправильна, тому, виділивши з неї цілу частину, отримаємо 111/12. Короткий рішення записується так:
ВІДПОВІДЬ: 111/12
ПРИКЛАД:
Віднімання змішаних дробів.
Щоб відняти змішані числа, спочатку наведемо дробові частини зменшуваного і від'ємника до найменшого спільного знаменника. Потім віднімемо ціле з цілого і дріб з дробу.
ПРИКЛАД:
Знайти різницю:РОЗВ'ЯЗАННЯ:
ВІДПОВІДЬ: 413/22
ПРИКЛАД:
Але бувають випадки, коли дрібна частина від'ємника більше дробової частини зменшуваного. У таких випадках потрібно взяти одну одиницю з цілої частини зменшуваного, роздрібнити її в ті частки, в яких виражена дрібна частина, і додати до дробової частини зменшуваного. А потім віднімання буде виконуватися так само, як віднімання мішаних чисел.
ПРИКЛАД:
У разі, коли дріб від'ємника більше, ніж дріб зменшуваного, надходять у такий спосіб: беруть одну одиницю (ціле) з цілого числа зменшуваного, записують його як неправильну дріб, чисельник і знаменник якої рівні між собою і дорівнюють знаменника дробової частини, і додають до дробової частини, далі забирають дві змішані дроби.
ПРИКЛАД:
Виконати віднімання:РОЗВ'ЯЗАННЯ:
Дріб 4/9
менше ніж дріб 11/12 так як
4 ∙ 12 = 36 < 9 ∙ 11 = 99,
тодіВІДПОВІДЬ: 319/36
Віднімання звичайного дробу з натурального числа.
Віднімання звичайного дробу з натурального числа можна звести до віднімання звичайних дробів, представивши натуральне число як дріб.
ПРИКЛАД:
Відніміть звичайну дріб 5/3 від натурального числа 7.
РОЗВ'ЯЗАННЯ:
Уявімо число 7 як дріб 7/1, після чого виконаємо віднімання:
Виділивши цілу частину з отриманої дробу, отримуємо остаточну відповідь.
ВІДПОВІДЬ: 51/3
Розглянемо ще приклад на віднімання змішаного числа з натурального числа.
ПРИКЛАД:
Але існує більш раціональний спосіб віднімання дробу з натурального числа. Його переваги помітні тоді, коли зменшуване натуральне число і знаменник віднімається дробу є великими числами. Якщо віднімається дріб правильна, то зменшуване натуральне число можна замінити сумою двох чисел, одне з яких дорівнює одиниці, відняти правильну дріб від одиниці, після чого завершити обчислення.
ПРИКЛАД:
Знайти різницю:
РОЗВ'ЯЗАННЯ:
Виконаємо віднімання дробів за описаним вище правилом:
ВІДПОВІДЬ: 2/5
ПРИКЛАД:
Виконайте віднімання звичайного дробу 13/62 з натурального числа 1065.
РОЗВ'ЯЗАННЯ:
Віднімається звичайна дріб – правильна. Замінимо число 1065 сумою
1064 + 1,
При цьому отримаємо:
Залишилося обчислити значення отриманого виразу. В силу властивостей віднімання, отриманий вираз можна переписати так:
Обчислимо значення різниці в дужках, замінивши одиницю дробом, 1/1:
Короткий рішення записується так:
ВІДПОВІДЬ: 106449/62
Розглянемо ще приклад на віднімання змішаного числа з цілого числа.
ПРИКЛАД:
Якщо ж віднімається дріб неправильна, то її можна замінити змішаним числом, після чого провести віднімання змішаного числа з натурального числа.
ПРИКЛАД:
Відніміть
звичайну дріб 73/5 від натурального числа 644.
РОЗВ'ЯЗАННЯ:
Тоді
ВІДПОВІДЬ: 6292/5
Віднімання
натурального числа з звичайного дробу.
Віднімання натурального числа з дробу можна звести
до віднімання звичайних дробів. Для цього достатньо уявити натуральне число у
вигляді дробу зі знаменником 1.
Віднімання натурального числа з неправильного дробу
зручніше проводити, представивши дріб у вигляді змішаного числа.
ПРИКЛАД:
Відніміть
число 3
від дробу 83/21.
РОЗВ'ЯЗАННЯ:
Спочатку виділимо цілу
частину з неправильного дробу 83/21, отримаємо:
тодіЗалишилося провести віднімання натурального числа з змішаного числа: ВІДПОВІДЬ: 20/21
Поширення
властивостей віднімання на дробові числа.
Всі закони і властивості віднімання натуральних
чисел справедливі і для дробових чисел. Їх застосування в багатьох випадках
значно спрощує процес обчислення.
Замість того, щоб відняти суму дробів, можна відняти
кожний доданок послідовно, і назад: замість того, щоб вичитати кожне число
послідовно, можна відняти відразу їх суму.
ПРИКЛАД:
Обчисліть значення виразу:
РОЗВ'ЯЗАННЯ:
Спочатку обчислимо різницю
Після чого від неї віднімемо дріб 5/6.
Після виділення цілої частини з отриманої неправильної дробу отримаємо:
ВІДПОВІДЬ: 311/12
ПРИКЛАД:
Тут використано правило вирахування з чисел різниці.
РОЗВ'ЯЗАННЯ:
Тут використано правило вирахування з чисел різниці.
Коли вираз містить і натуральні числа і дроби, то
при обчисленні зручно групувати числа з числами, а дроби з дробом.
ПРИКЛАД:
Виконайте віднімання суми натурального числа і
звичайного дробу
з суми натурального числа і дробиРОЗВ'ЯЗАННЯ:
Нам потрібно обчислити
різницю
Властивості додавання і віднімання дозволяють нам провести таку угруповання
що спрощує обчислення. Залишилося лише закінчити обчислення:
ВІДПОВІДЬ: 931/4
Властивості додавання і віднімання дозволяють нам провести таку угруповання
що спрощує обчислення. Залишилося лише закінчити обчислення:
ВІДПОВІДЬ: 931/4
Якщо зменшуване зменшимо на яке-небудь число, не
змінюючи від'ємника, то різниця зменшиться на те ж саме число.
Якщо від'ємник збільшимо на яке-небудь число, то різниця
зменшиться на те ж число.
Якщо від'ємник зменшимо на яке-небудь число, то
різниця збільшиться на стільки ж побільшало.
Якщо зменшуване і
від'ємник збільшимо або зменшимо на одне і те ж число, то різниця не зміниться.
Завдання до уроку 16
Інші уроки:
- Урок 1. Нумерація
- Урок 2. Додавання натуральних чисел
- Урок 3. Віднімання натуральних чисел
- Урок 4. Таблиця множення
- Урок 5. Множення натуральних чисел
- Урок 6. Ділення натуральних чисел
- Урок 7. Степінь числа
- Урок 8. Вимірювання величин
- Урок 9. Ділення с остачею
- Урок 10. Подільність натуральних чисел
- Урок 11. Найбільшій спільний дільник (НСД)
- Урок 12. Найменше спільне кратне (НСК)
- Урок 13. Звичайні дроби
- Урок 14. Перетворення дробів
- Урок 15. Додавання дробів
- Урок 17. Множення дробів
- Урок 18. Ділення дробів
- Урок 19. Знаходження дробу від числа (задачи)
- Урок 20. Знаходження числа за відомою його частиною (задачи)
- Урок 21. Кінечни десяткові дроби
- Урок 22. Додавання десяткових дробів
- Урок 23. Віднимання десяткових дробів
- Урок 24. Множення десяткових дробів
- Урок 25. Ділення десяткових дробів
- Урок 26. Округлення чисел








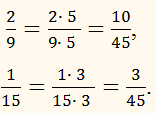



































Комментариев нет:
Отправить комментарий