Уроки математики и физики (RU + UA)

▼

суббота, 12 декабря 2015 г.

Урок 8. Действия над выражениями в которых находятся квадратные корни

Выражения, в которых находятся квадратные корни, можно складывать, отнимать, умножать и делить (на знаменатель отличный от нуля), а также возводить в степень.

 Подобие радикалов.

 Два или несколько радикалов называются подобными, если они одинаковой степени и имеют одинаковые подкоренные выражения.

 Иногда данные радикалы оказываются подобными только после некоторых преобразований.

 ПРИМЕР:

 Подобны ли радикалы ?
РЕШЕНИЕ:
ОТВЕТ:

 Подобны.

 Сложение и вычитание.

 Чтобы сложить (или вычесть) радикалы, их соединяют знаками плюс (или минус) и приводят подобные члены, если они окажутся.

ПРИМЕР:
ПРИМЕР:
Найдите значение выражения:
ПРИМЕР:
Найдите значение выражения:
Так как

7 –  √͞͞͞͞͞11 ˃ 0,   3 –  √͞͞͞͞͞11 < 0, то,

учитывая определение модуля, получаем:

|7 –  √͞͞͞͞͞11|+|3 –  √͞͞͞͞͞11|=

= 7 –  √͞͞͞͞͞11 – (3 –  √͞͞͞͞͞11) = 4.

ПРИМЕР:

Упростите выражение:

6√͞͞͞͞͞8  – √͞͞͞͞͞32.

РЕШЕНИЕ:

6√͞͞͞͞͞8  – √͞͞͞͞͞32 = 12√͞͞͞͞͞2  – 4√͞͞͞͞͞2  = 8√͞͞͞͞͞2.

ПРИМЕР:

Упростите выражение:

10√͞͞͞͞͞3  – 0,5√͞͞͞͞͞48.

РЕШЕНИЕ:

10√͞͞͞͞͞3  – 0,5√͞͞͞͞͞48 = 10√͞͞͞͞͞3  – 0,5 ∙ 4√͞͞͞͞͞3  =

= 10√͞͞͞͞͞3  – 2√͞͞͞͞͞3  = 8√͞͞͞͞͞3.

ПРИМЕР:

Упростите выражение:

6√͞͞͞͞͞18  – 4√͞͞͞͞͞8.

РЕШЕНИЕ:

6√͞͞͞͞͞18  – 4√͞͞͞͞͞8 = 6 ∙ 3√͞͞͞͞͞2  – 4 ∙ 2√͞͞͞͞͞2  =

= 18√͞͞͞͞͞2  – 8√͞͞͞͞͞2  = 10√͞͞͞͞͞2.

ПРИМЕР:

Упростить выражение:
ПРИМЕР:

 Выполните указанные действия:
РЕШЕНИЕ:
ПРИМЕР:

 Вычислить:
РЕШЕНИЕ:

27 + 10√͞͞͞͞͞2 = (√͞͞͞͞͞2 + 5)2,
27 – 10√͞͞͞͞͞2 = (√͞͞͞͞͞2 – 5)2.

 Отсюда
ОТВЕТ:  10

ПРИМЕР:

 Вычислить:
РЕШЕНИЕ:

 Подкоренные выражения не являются полными квадратами, то есть применить приём из предыдущего примера не удастся. Возведём вычисляемое выражение в квадрат:
Следовательно, исходное выражение может быть равно  6  или  –6. Так как
То это выражение отрицательно.

 ОТВЕТ:  –6 

ПРИМЕР:

Упростить выражение:
РЕШЕНИЕ:
Имеем:
Поскольку заданное выражение содержит слагаемое
то  2 – х ≥ 0, откуда находим, что  х ≤ 2.

Значит, х – 3 < 0 , а потому

|х – 3| = –(х – 3) = 3 – х.

Итак,
и мы получаем
Умножение.

Чтобы перемножить несколько радикалов одинаковой степени, надо перемножить подкоренные выражения и из произведения извлечь корень той же степени.

ПРИМЕР:

Выполнить умножение:

РЕШЕНИЕ:
ПРИМЕР:

 Выполнить умножение:
РЕШЕНИЕ:
Деление.

 Чтобы разделить радикалы с одинаковыми показателями, надо разделить их подкоренные выражения и из частного извлечь корень той же степени.

 ПРИМЕР:

 Выполнить деление:
РЕШЕНИЕ:

ПРИМЕР:

Упростить выражение:

РЕШЕНИЕ:
Задания к уроку 8
Другие уроки:
на

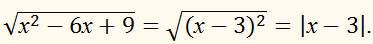
Комментариев нет:

Отправить комментарий