Уроки математики и физики (RU + UA)

▼

среда, 20 января 2016 г.

Урок 16. Действия над радикалами m-степени

Подобие радикалов.

 Два или несколько радикалов называются подобными, если они одинаковой степени и имеют одинаковые подкоренные выражения.

ПРИМЕР:
подобные радикалы, так как они оба третьей степени и имеют одинаковые подкоренные выражения  х2с.

 Иногда данные радикалы оказываются подобными только после некоторых преобразований.

 ПРИМЕР:

 Подобны ли радикалы ?
Не подобны.

 Сложение и вычитание.

 Чтобы сложить (или вычесть) радикалы, их соединяют знаками плюс (или минус) и приводят подобные члены, если они окажутся.

 ПРИМЕР:

ПРИМЕР:

Вычислите:
РЕШЕНИЕ:
ПРИМЕР:
Вычислите:
РЕШЕНИЕ:
Алгебраические суммы радикалов можно возводить в степень, пользуясь формулами сокращённого умножения.
ПРИМЕР:
Умножение.

 Чтобы перемножить несколько радикалов одинаковой степени, надо перемножить подкоренные выражения и из произведения извлечь корень той же степени.

 Если перемножаются радикалы с различными показателями, то их надо предварительно привести к одному показателю

 Если перед радикалами имеются коэффициенты, то их перемножают.

ПРИМЕР:

Упростить:
РЕШЕНИЕ:

Для перемножения корней одной и той же степени достаточно перемножить подкоренные выражения и из полученного результата извлечь корень той же степени.
ПРИМЕР:
Упростить:
РЕШЕНИЕ:
Прежде всего, нужно привести радикалы к одному показателю. Мы можем показатель корня и показатель степени подкоренного выражения умножить на одно и то же натуральное число. Поэтому:
Далее имеем:
А теперь в полученном результате разделим показатели корня и степени подкоренного выражения на  3.
Итак:
ПРИМЕР:
ПРИМЕР:

ПРИМЕР:

Найдите значение выражения:
РЕШЕНИЕ:

Запишем выражение  49 + 20√͞͞͞͞͞6  как квадрат двучлена:
Деление.

Чтобы разделить радикалы с одинаковыми показателями, надо разделить их подкоренные выражения и из частного извлечь корень той же степени.

 Чтобы разделить радикалы с различными показателями, их надо привести предварительно е одинаковым показателям.

 Если есть коэффициенты, то их делят.

ПРИМЕР:
ПРИМЕР:

 Выполнить деление с помощью формул сокращённого умножения.

ПРИМЕР:
РЕШЕНИЕ:

При решении задач на упрощение иррациональных алгебраических выражений часто применяют способ замены младших степеней переменных какими-либо новыми переменными. При этом должно получиться рациональное алгебраическое выражение относительно новых переменных. Упростив полученное выражение, следует вернуться к выражению с прежними переменными.
Обозначим
Упростим выражение, используя свойства степеней, правила действий с корнями и новые обозначения:
ОТВЕТ:  –1 

 Задания к уроку 16
Другие уроки:
на

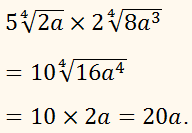
Комментариев нет:

Отправить комментарий