Раньше было введено
понятие корня второй степени. Но в математике рассматриваются корни не только
второй, но и третьей, четвёртой, пятой и вообще
m-й
степени. Пусть m – произвольное натуральное число больше 1,
а а – любое действительное число.
Корнем m – степени из числа a называется такое число, m – я степень которого равна а.
ПРИМЕР:
Корень 3-й степени из 64 равен 4, так как 43 = 64.
Корень 5-й степени из
–32 равен –2,
так как (–2)3 = –32.
Корень 4-й степени из
81 имеет (в множестве действительных чисел) два значения: –3 и 3 так как:
(–3)4 = 81 и 34 = 81.
Корень m-й
степени из числа а обозначается символом:
ПРИМЕР:
Следовательно,
только при
отрицательном а и нечётном m имеет отрицательное значение. При
положительном а числовсегда положительно. Если же а < 0 , а m чётное, то
(в множестве действительных чисел) не существует.
ПРИМЕР:
так как 25 = 32;ибо (–5)3 = –125.ПРИМЕР:
– арифметический корень,– не арифметический корень.При любом
натуральном n корень из 0 равен 0.
ПРИМЕР:При любом натуральном n корень из 1 равен 1.
ПРИМЕР:
Очевидно, что при всех значениях а, при которых выражение
имеет смысл, истинно равенство:
Корень второй степени принято называть квадратным корнем, а корень третьей степени – кубическим корнем.
Корень нечётной
степени из отрицательного числа можно выразить через арифметический корень той
же степени из противоположного (положительного) числа.
ПРИМЕР:
ПРИМЕР:ПРИМЕР:
Запись
ПРИМЕР:
Другие уроки:
- Урок 1. Действительные числа
- Урок 2. Арифметический квадратный корень
- Урок 3. Квалратный корень из произведения и дроби
- Урок 4. Квадратный корень из степени
- Урок 5. Вынесение множителя из-под знака корня
- Урок 6. Внесение множителя под знак корня
- Урок 7. Избавление от иррациональности в знаменателе дроби
- Урок 8. Действия над радикалами
- Урок 9. Возведение в степень арифметических квадратніх корней
- Урок 11. Корень m-й степени из произведения
- Урок 12. Корень m-й степени из дроби
- Урок 13. Корень m-й степени из степени
- Урок 14. Вынесение множителя из-под знака корня m-й степени
- Урок 15. Внесение множителуй под знак корня m-й степени
- Урок 16. Действия над радикалами m-й степени
- Урок 17. Возведение в степень корня m-й степени
- Урок 18. Извлечение корня из корня m-й степени
- Урок 19. Избавление от иррациональности в числителе или знпменателе дроби
- Урок 20. Основное свойство радикала
- Урок 21. Преобразование выражений содержащих степени с положительными дробными показателями
- Урок 22. Преобразование выражений содержащих степени с отрицательными дробными показателями
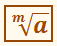




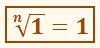








Комментариев нет:
Отправить комментарий