На підставі формул
sin (х + у) = sin х cos у + cos х sin у,
sin (х– у) = sin х cos у – cos х sin у,
в результаті почленного складання та віднімання цих
рівностей отримаємо:
sin (х + у) + sin (х – у)
= 2 sin х cos у,
sin (х + у) – sin (х – у)
= 2 cos
х sin у.
Покладемо у цих рівностях
х + у = α,
х – у = β.
Вирішуючи ці два рівняння щодо х і у, знаходимо:
У рівностіsin (х + у) + sin (х – у)
= 2 sin х cos у,
sin (х + у) – sin (х – у)
= 2 cos
х sin у
Перетворити
на добуток:
1 +
sin α.
Перетворити
на добуток:
1 + 2 sin α.
В отриманих рівностях α і β – будь-які кути,
оскільки які б не були α
та β, завжди знайдуться такі х і
у, для яких
х + у
= α,
х – у = β.
Перетворити
на добуток:
√͞͞͞͞͞3 – 2
sin α.
РОЗВ'ЯЗАННЯ:
Перетворити
на добуток:
sin2 α – sin2 β.
РОЗВ'ЯЗАННЯ:

ПРИКЛАД:
Перетворити
на добуток:
sin х + соs 2х – sin 3х.
РОЗВ'ЯЗАННЯ:
sin х + соs 2х – sin 3х = соs 2х – (sin 3х – sin х) =
cos (х + у) = cos х cos у – sin х sin у.
соs (х – у) = соs х
cos у + sin х sin у.
Почленное складання цих рівностей дає таке співвідношення:
cos (х + у)
+ cos (х – у) = 2 соs х
cos у,
Якщо в кожній з цих рівностей перейти від х і у до α і β на
підставі рівностей
х + у = α,
ПРИКЛАД:
Перетворити
на добуток:
соs 48° + соs 12°.
РОЗВ'ЯЗАННЯ:
Запишемо формули косинуса суми та косинуса різниці двох кутів:
cos (х + у) = cos х cos у – sin х sin у.
соs (х – у) = соs х
cos у + sin х sin у.
Почленное віднімання цих рівностей дає таке співвідношення:
cos (х + у)
– cos (х – у) = –2 sin х sin у.
Якщо в кожній з цих рівностей перейти від х і у
до α і β на підставі рівностей
х + у = α,
ПРИКЛАД:
Перетворити
на добуток:
соs 48° – соs 12°.
РОЗВ'ЯЗАННЯ:
Застосувавши
формулу різниці косинусів при
α =
48°, β = 12°,
ПРИКЛАД:
Перетворити
на добуток:
соs 5° – соs 35°.
ПРИМЕР:
Перетворити
на добуток:
cos2 α – cos2 β.
РОЗВ'ЯЗАННЯ:
Довести тотожність.
ПРИКЛАД:
Тими ж формулами можна скористатися для перетворення на добуток
сум та різниць виду
sin
α + соs β,
sin
α – соs β.
ПРИКЛАД:
Перетворити
на добуток:
sin α + соs α.
РОЗВ'ЯЗАННЯ:
sin α + соs α
= sin α
+ sin (90° – α) =
= 2 sin 45° соs (45°
– α) = √͞͞͞͞͞2
соs (45° – α).
ПРИКЛАД:
Різниця
sin
96° – соs 36°
можна
замінити різницею
sin
96° – sin 54°,
Суму
соs 10°
+ sin 100°
можна
замінити сумою
sin
80° + sin 100° =
Перетворити
на добуток:
1 + sin α + соs α.
РОЗВ'ЯЗАННЯ:
1 + sin α + соs α
= (1 + соs α)
+ sin α
=
= 2 соs2 α/2 + 2 sin α/2 соs α/2 =
= 2 соs α/2
(соs α/2
+ sin α/2)
=
= 2 соs α/2
[sin (π/2 – α/2) + sin α/2]
=
= 2 соs α/2
2 sin π/4 cos (π/4 – α/2) =
= 2√͞͞͞͞͞2
cos α/2 cos (π/4 – α/2).
Перетворення
на добуток суми та різниці двох тангенсів або котангенсів.
Аналогічно перетворюється на добуток різниця тангенсів кутів α і β:
В результаті складання котангенсів двох кутів отримаємо:
ПРИКЛАД:
Перетворити
на добуток:
tg
20° + tg 70°.
РОЗВ'ЯЗАННЯ:
Довести,
що
tg
9° – tg 27° – tg
63° + tg 81° = 4.
ДОКАЗАТЕЛЬСТВО:
tg
9° – tg 27° – tg
63° + tg 81° =
= (tg
9° + tg 81°) – (tg
27° + tg 63°).
З формули
sin (х + у) + sin (х – у)
= 2 sin х cos у,
слід
ПРИКЛАД:
Перетворити
на суму добуток:
sin
43° cos 19°.
РОЗВ'ЯЗАННЯ:
1/2 (sin
62° + sin 24°)
ПРИКЛАД:
Перетворити
на суму добуток:
sin
50° cos 30°.
РОЗВ'ЯЗАННЯ:
sin
50° cos 30° = 1/2 (sin 80° + sin 20°).
З
формули
cos (х + у) + cos (х – у) = 2 соs х
cos у
ПРИКЛАД:
Перетворити
на суму добуток:
cos
25° cos 59°.
РОЗВ'ЯЗАННЯ:
cos
25° cos 59° = 1/2 (cos 84° + cos 34°).
ПРИКЛАД:
Знайти
період функції:
у
= cos х cos 6х.
РОЗВ'ЯЗАННЯ:
Скориставшись
формулою
cos х
cos у = 1/2 [cos (х + у) + cos (х – у)]
отримаємо
у
= cos х cos 6х =
1/2 [cos (х – 6х) + cos (х + 6х)]
=
= 1/2
cos 5х + 1/2
cos 7х.
Період
функції
у
= cos 5х,
равен
Т1 =
2π/5.
Період
функції
у
= cos 7х,
дорівнює
Т2 =
2π/7.
Найменше
число, при розподілі якого на
Т1 = 2π/5 і Т2 = 2π/7
виходять
цілі числа, число 2π. Отже, період заданої функції дорівнює Т =
2π.
ВІДПОВІДЬ: 2π
З формули
cos (х + у)
– cos (х – у) = –2 sin х sin у,
ПРИКЛАД:
Перетворити
на суму добуток:
sin 70° sin 15°.
РОЗВ'ЯЗАННЯ:
sin 70° sin 15° = 1/2 (cos 55° – cos 85°).
ПРИКЛАД:
Спростити
вираз:
A
= sin 3α sin3 α + cos 3α cos3 α.
РОЗВ'ЯЗАННЯ:
Перетворимо
цей вираз таким чином:
A
= (sin 3α sin α) sin2 α +
(cos 3α cos α) cos2 α.
A
= 1/2 (cos
2α – cos 4α) sin2 α + 1/2
(cos 2α + cos 4α) cos2 α =
1/2 cos 2α (sin2 α + cos2 α) + 1/2 cos
4α (cos2 α – sin2 α) =
1/2 cos 2α + 1/2 cos 4α cos 2α = 1/2 cos 2α (1
+ cos 4α) =
1/2 cos 2α 2cos2 2α = cos3 2α.
ПРИКЛАД:
Довести
тотожність:
1 – cos α – sin
α = 2√͞͞͞͞͞2 sin α/2 sin (α/2 – π/4).
РОЗВ'ЯЗАННЯ:
Перетворимо
праву частину рівності:
2√͞͞͞͞͞2 sin α/2 sin (α/2 – π/4) =
=
2√͞͞͞͞͞2 sin α/2 (sin α/2 cos
π/4 – sin α/2 cos π/4) =
=
2
sin2 α/2 – 2 sin α/2 cos α/2 = 1 – cos α – sin
α.
- Урок 1. Градусний вимір кутових величин
- Урок 2. Радіанне вимірювання кутових величин
- Урок 3. Основні тригонометричні функції
- Урок 4. Натуральні тригонометричні таблиці
- Урок 5. Періодичність тригонометричних функції
- Урок 6. Область визначення і область значення тригонометричних функцій
- Урок 7. Знаки тригонометричних функцій
- Урок 8. Парність і непарність тригонометричних функцій
- Урок 9. Тригонометричні функції деяких кутів
- Урок 10. Побудова кута за даним значенням його тригонометричної функції
- Урок 11. Основні тригонометричні тотожності
- Урок 12. Вирази всіх тригонометричних функцій через одну з них
- Урок 13. Розв'язання прямокутних і рівнобедрених трикутників за допомогою тригонометричних функцій
- Урок 14. Теорема синусів
- Урок 15. Теорема косинусів
- Урок 16. Рішення косокутних трикутників
- Урок 17. Приклади рішення завдань з планіметрії із застосуванням тригонометрії
- Урок 18. Рішення практичних завдань за допомогою тригонометрії
- Урок 19. Формули зведення (1)
- Урок 20. Формули зведення (2)
- Урок 21. Формули додавання і віднімання аргументів тригонометричних функцій
- Урок 22. Формули подвійних і потрійних кутів (аргументів)
- Урок 23. Формули половинного аргументу
- Урок 25. Графіки функції y = sin x і y = cos x
- Урок 26. Графіки функції y = tg x і ctg x
- Урок 27. Обернені тригонометричні функції
- Урок 28. Основні тотожності зворотних тригонометричних функцій
- Урок 29. Вираз одній з аркфункцій через інші
- Урок 30. Графіки зворотних тригонометричних функцій
- Урок 31. Побудова графіків тригонометричних функцій методом геометричних перетворень







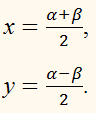

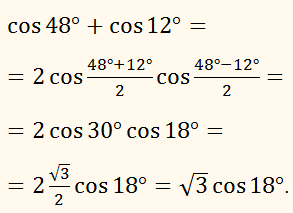






























Комментариев нет:
Отправить комментарий