Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
ФОРМУЛИ ПЕРЕТВОРЕННЯ СУМИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ В ДОБУТОК
або
ВІДЕО УРОКОМ
1. Перетворіть у добуток вираз:
1 – cos
15°.
а) 2 sin2
7°30ʹ;
б) cos2
7°30ʹ;
в) 2 cos2
7°30ʹ;
г) sin2
7°30ʹ.
б) 2 cos
(π/6 – x/2) sin (π/6 – x/2);
в) 2 cos
(π/6 + x/2) sin (π/6 – x/2);
г) 2 cos
(π/6 + x/2) sin (π/6 + x/2).
б) 2 cos (π/8 + α/2) cos (π/8 – α/2);
в) 2 cos (π/8 + α/2) cos (π/8 + α/2);
г) 2 cos (π/8 – α/2) cos (π/8 – α/2).
4. Перетворіть
у добуток вираз:
1 + sin φ + cos φ.
а) 2√͞͞͞͞͞2
cos φ/2 cos (π/4 – φ/2);
б) 2√͞͞͞͞͞2
cos φ/2 sin (π/4 – φ/2);
в) 2√͞͞͞͞͞2
sin φ/2 sin (π/4 – φ/2);
г) 2√͞͞͞͞͞2
sin φ/2 cos (π/4 – φ/2).
7.
Перетворіть у добуток вираз:
1 + sin φ – cos φ.
а) 2√͞͞͞͞͞2
cos φ/2 cos (π/4 – φ/2);
б) 2√͞͞͞͞͞2
sin φ/2 cos (π/4 – φ/2);
в) 2√͞͞͞͞͞2
cos φ/2 sin (π/4 – φ/2);
г) 2√͞͞͞͞͞2
sin φ/2 sin (π/4 – φ/2).
б) 4 sin
8α;
в) 2 sin 8α;
г) 4 cos
8α.
9. Спростіть вираз:
sin (π – α) sin(3π/2 – α).
а) –1/2 sin
2α;
б) 1/2 cos 2α;
в) –1/2 cos 2α;
г) 1/2 sin 2α.
10. Перетворіть
у добуток вираз:
sin 4α + sin 2α.
а) 2 sin 3α sin α;
б) 2 sin α cos 3α;
в) 2 sin 3α cos α;
г) 2 cos 3α cos α.
б) sin α;
в) cos α;
г) sin 4α.
12. Спростити
вираз:
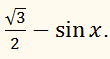






Комментариев нет:
Отправить комментарий