Уроки математики и физики (RU + UA)

▼

четверг, 23 февраля 2017 г.

Урок 21. Перетворення виразів, що містять степеня з позитивними дробними показниками

Степенем позитивного числа з раціональним показником

де  m – ціле число, а  n – натуральне  (n > 1), називають корінь  n-го степеня з числа  am.
ПРИКЛАД:
Якщо  а > 0  і  х – довільне дробове число, подане у виглядіде  m – целое, а  n – натуральне, то:
Якщо  а = 0  і  х – дробове позитивне число, то: 

ax = 0. 

Формулу
в елементарній математиці звичайно розглядають тільки при  а ≥ 0, оскільки при від’ємних значеннях вираз
а отже, і
може не мати значення (в множині дійсних чисел). Дробові показники можуть бути будь-якими раціональними числами.

ПРИКЛАД:

Такі вирази, як:
немає сенсу.

Те саме дробове число можна представити у вигляді дробу з цілим чисельником і натуральним знаменником різними способами.

ПРИКЛАД:

Дробове число  0,75  можна подати у вигляді дробу так:
і так далі

Значення степеня з дробовим показником залежить від вибору способу запису числа  x  як дробу; представляючи дробове число  х  як ставлення цілого числа до натурального різними способами, завжди отримуватимемо той самий результат.

ПРИКЛАД:

Нехай  а > 0. Тоді
і значить,a ≥ 0, n ∈ N,  n ≥ 2.
ПРИКЛАД:
ПРИКЛАД:
ПРИКЛАД:
ПРИКЛАД:
Якщо основи степенів позитивні, то властивості степеня з цілим показником залишаються справедливими і для степенів з будь-яким дробовим показником. 

Дії над степенями з будь-якими раціональними показниками виконують за тими самими правилами, що й дії над степенями з натуральними показниками.

Для будь-яких раціональних  u  та  v  та дійсного  a > 0 вірні рівності:

ПРИКЛАД:

Спростити вираз:
РОЗВ'ЯЗАННЯ:

Наведемо радикали до одного показника. Для цього потрібно знайти найменше загальне кратне чисел  8  та  12, тобто

НОК(8, 12) = 24.

Далі показники кореня та степеня підкореного виразу для першого з перемножуваних радикалів слід помножити на  3, а для другого – на  2. Отримаємо:
Насправді при виконанні дій над радикалами досить часто переходять до дробових показників. Наприклад:
ПРИКЛАД:
Скоротити дріб:
Даний дріб визначений при  х > 0. Розкладемо на множники чисельник і знаменник дробу і скоротимо його:
Вираз
тотожно дорівнює початковому на безлічі позитивних значень х, тобто на області визначення вихідного дробу.

ПРИКЛАД:

Чому дорівнює значення виразу ?
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Спростіть вираз:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Чому дорівнює значення виразу:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Спростить:
РОЗВ'ЯЗАННЯ:

ВІДПОВІДЬ:
Завдання до уроку 21
Інші уроки:
на

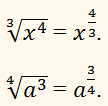
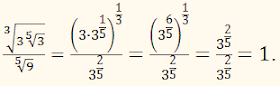
Комментариев нет:

Отправить комментарий