ВИДЕОУРОК
Сила – это
физическое явление, способное изменить форму материальных тел, вызывать их
движение, менять направление и скорость движения этих тел или приводить тело в
состояние покоя.
ПРИМЕР:
Ребята слепили снеговика, а хулиганы его разрушили. Получается, что
хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы
снеговика.
На дворе стояла тележка. Прохожий случайно задел её, и тележка сдвинулась
с места. Получается, что прохожий применил силу к тележке и вызвал её движение.
Далее тот же прохожий остановил тележку, чтобы она далеко не уехала.
Получается, что прохожий применил силу, тем самым привёл тележку в состояние
покоя.
Сила является физической
величиной – мерой воздействия на тело других тел. Сила обозначается буквой F.
Что такое работа ?
Работа – это количественная
мера действия силы на тело. Работа зависит от количества силы, приложенной на
тело и от направления этой силы, а так же от перемещения данного тела.
ПРИМЕР:
Если мы попробуем сдвинуть шкаф с места, и он сдвинется, то можно
сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела
к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не
сдвинется, а значит и работа не будет совершена, поскольку сила была приложена,
но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной
латинской буквой А.
Совместная работа возникает,
когда несколько человек (бригад, насосов и так далее) выполняют одну и ту же
работу вместе, причём работают с разными скоростями.
В таких задачах всегда
присутствуют одни и те же величины, их три:
Первая величина – это время, за которое выполняется та или иная работа. Обозначают время буквой t.
Вторая величина – объём работы, то есть, сколько сделано деталей, налито воды, вспахано полей и так
далее. Обозначают объём работы буквой А.
Третья величина – производительность. По сути это скорость работы.
Скорость любой работы, то есть
производительность, можно определить, как объём работы, сделанной за какое-то
время.
Производительностью
называют работу, выполненную за единицу времени.
Под единицей
подразумевается 1 час, 1 мин, 1 сек.
Обозначают производительность
буквой П.
Если известны работа и время
работы, то можно найти производительность.
Чтобы найти
производительность, надо выполненную работу разделить на время работы.
Формула для производительности:
П = А
: t.
ПРИМЕР:
Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 мин, а второй
15 булочек за 5 мин. Как узнать, кто из пекарей работал быстрее, первый или второй ?
РЕШЕНИЕ:
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят,
что у него производительность больше. Зная правило или формулу нахождения
производительности, можно определить, сколько булочек приходится на одну
минуту.
Найдём производительность первого пекаря. Разделим работу, которую он
выполнил, на время, которое он на неё потратил. Выполненная работа это
количество испечённых им булочек, то есть
40, а время – 10 мин.
40 : 10 = 4 булочки в минуту.
Аналогично найдём производительность второго пекаря. Разделим 15 на 5:
15 : 5 = 3 булочки в минуту.
Первый пекарь в минуту выпекает больше булочек, чем второй, значит его
производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В
этом случае решение принимает следующий вид:
Ппервого пекаря = А
: t = 40 : 10 = 4 бул./мин.
Пвторого пекаря = А
: t = 15 : 5 = 3 бул./мин.
ЗАДАЧА:
Принтер напечатал 350
страниц за 5 часов. С какой производительностью он работал ?
РЕШЕНИЕ:
Если в течении 5
часов принтер напечатал 350 страниц, то в течении часа он напечатал 350
: 5. То есть работал с
производительностью 70 страниц в час:
350 : 5 = 70 стр./час.
Также, решение можно записать с
помощью формулы нахождения производительности:
П = А : t = 350 : 5
= 70 стр./час.
ЗАДАЧА:
Папа выполняет всю работу за 4 час, а его сын – за
7 час. Какую часть
работы они сделают вместе за 1 час ?
РЕШЕНИЕ:
Пусть вся работа равна 1. Тогда производительность папы:
1 : 4 = 1/4,
а производительность сына:
1 : 7 = 1/7.
Производительность общая:
1/4 + 1/7 = 7/28 + 4/28 = 11/28.
Иногда слово <<производительность>>
может быть заменена на слово <<скорость>>, <<эффективность>>,
<<продуктивность>>, <<плодотворность>>.
ЗАДАЧА:
Пете нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью
12 страниц в час. С
какой скоростью ему надо читать оставшуюся часть книги, если у него есть на
это 4 часа ?
РЕШЕНИЕ:
Узнаем, сколько страниц Петя прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый
день, нужно 12 умножить
на 4.
12 ∙ 4 = 48 страниц прочитал в
первый день.
Узнаем, сколько страниц осталось почитать. Вычтем из общего количества
страниц (100) количество прочитанных страниц (48).
100 – 48 = 52 (стр.).
Осталось прочесть 52 страницы. Теперь найдём такую производительность,
при которой Петя сможет прочитать 52 страницы за 4 часа. Раскидаем
52 страницы на 4 часа поровну:
52 : 4 = 13 страниц в час.
Если известны производительность и время работы, то можно найти выполненную
работу.
Выполненная работа равна производительности умноженной
на время работы.
Формула для работы:
А = П∙ t.
ПРИМЕР:
Если производительность пекаря
составляет 50 булочек в час, и он
проработал 4 час, то можно найти всю
выполненную работу за эти четыре часа. Для этого производительность (50 бул./час) нужно умножить на время его работы (4 час):
50 ∙ 4 = 200 булочек.
ЗАДАЧА:
Принтер работает с
производительностью 70 стр./час. Сколько страниц он напечатает за 5 часов ?
РЕШЕНИЕ:
Если в час принтер
печатает 70
страниц, то за 5 часов он напечатает в
5
раз больше:
70 ∙ 5 = 350 страниц.
Также, решение можно записать с
помощью формулы нахождения работы. В данном случае, количество напечатанных
страниц является выполненной работой:
А = П ∙ t = 70 ∙ 5
= 350 страниц.
ЗАДАЧА:
Через первую трубу бассейн можно заполнить за 20
часов, а через вторую за 30 часов. Какая часть бассейна заполнится через обе трубы
за 1
час ?
РЕШЕНИЕ:
Работа в данном случае это заполнение бассейна. Обозначим
эту работу через единицу:
А = 1.
На прокладку траншеи требуется затратить 10
час. Экскаватор проработал 8 час, после чего ему осталось пройти 50
м. Найдите общую длину траншеи.
РЕШЕНИЕ:
В задаче подразумевается, что экскаватор работал с
одинаковой производительностью на протяжении всей работы. На работу требовалось
затратить 10 час. Проработано было
8
час. Значит, осталось ещё 2 час. На 2 часа приходится оставшиеся 50
м траншеи. Если разделить 50
м на
2,
то можно определить, сколько метров экскаватор прокладывает за один час.
50 : 2 = 25 м/час.
В час экскаватор прокладывал 25
м. Работал он 10 час. Умножим 25 на 10, мы определим общую длину траншеи.
25 ∙ 10 = 250 м.
Если известны работа и производительность, то можно найти время работы.
Время работы равно отношению выполненной работы к
производительности.
Формула для нахождения времени:
t = А : П.
ПРИМЕР:
Если в неделю бригада
отстраивает 2 этажа, то можно узнать, сколько недель потребуется для
отстройки 8 этажей. Чтобы определить время отстройки восьми этажей,
нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед.).
8 : 2 = 4 нед.
Если за неделю строится
2
этажа, то 8 этажей будет отстроено за четыре недели. В данном случае
вся работа была равна восьми. Производительность была равна двум, поскольку по
определению производительность есть работа, выполненная за единицу времени – в
нашем случае два этажа за неделю.
ЗАДАЧА:
Принтер работал с
производительностью 70 страниц в час и напечатал 350
страниц. Определите время работы принтера.
РЕШЕНИЕ:
Выражение <<принтер
работал с производительностью 70 страниц в час>> означает, что в каждом часе
принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не
напечатал 350 страниц. Очевидно, что разделив 350
страниц по 70, мы определим время работы принтера, то есть узнаем,
сколько часов он работал.
350 : 70 = 5 час.
Также, решение можно записать с
помощью формулы нахождения времени:
t = А : П
= 350 : 70 = 5 час
ЗАДАЧА:
Если 12 рабочих выполняют определённую работу за 3 дня, то за сколько дней эту же работу выполнят 4 рабочих, работая с одинаковой производительностью ?
РЕШЕНИЕ:
Так как в задаче говорится о работе
12 человек, то это
задача на совместную работу. Так как объём работы не известен, то примем его
за 1.
Пусть х частей работы в день – это производительность 1 рабочего. Совместная работа равна сумме
производительностей каждого из рабочих. Так как рабочих 12 и у них одинаковая
производительность, то:
П12 = 12П1 = 12х.
Воспользуемся формулой совместной производительности, согласно которой:
П = А : t.
Так как 12 рабочих выполнят работу за 3 дня, то:
t12 = 3 дня.
Подставим все значения в формулу:
12х = 1/3
Найдём х:
х = 1/36 – частей работы в день.
Итак, производительность 1-го
рабочего 1/36 частей работы в
день. Найдём время выполнения работы, когда работает 4 рабочих. Воспользуемся формулой времени:
t4 = А : П4.
Найдём производительность 4-х рабочих:
П4 = 4П1 = 4х = 4 ∙ 1/36 = 1/9.
Тогда:
t4 = А : П4 = 1 : 1/9 = 9 (дней).
ЗАДАЧА:
Одна труба может наполнить бассейн за четыре часа. Вторая – за шесть
часов. За какое время заполнится бассейн, если обе трубы включить одновременно ?
РЕШЕНИЕ:
Так как трубы работают вместе, складывают их производительности.
Для первой трубы, которая заполняет бассейн за 4 час:
П = А : t = 1 : 4 = 1/4 – за час
заполнит первая труба.
Для второй трубы, которая заполняет бассейн за 6 час:
П = А : t = 1 : 6 = 1/6 – за час
заполнит вторая труба.
Вместе, при совместной работе, трубы заполнят за час:
1/4 + 1/6 = 3/12 + 2/12 = 5/12 – две трубы
за один час.
Объём работы – 1 бассейн. Совместная производительность 5/12 бассейна в час. Тогда время заполнения
бассейна будет:
t =
А : П = 1 : 5/12 = 1 ∙ 12/5 = 12/5 (час).
ЗАДАЧА:
Лошадь съедает копну сена
за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и
овца вместе ?
РЕШЕНИЕ:
Работа в данном случае это
съедание копны сена. Обозначим её через единицу:
А = 1.
Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана
за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть
кран и вливать в него воду через шланг ?
РЕШЕНИЕ:
Работа в данном случае это наполнение сосуда. Обозначим эту работу через
единицу:
А = 1.
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг.Задания к уроку 23
- Урок 1. Отношение величин
- Урок 2. Пропорции
- Урок 3. Величины прямо пропорциональные
- Урок 4. Величины обратно пропорциональные
- Урок 5. Пропорциональное деление
- Урок 6. Проценты
- Урок 7. Нахождение процентов данного числа (задачи)
- Урок 8. Нахождение числа по его процентам (задачи)
- Урок 9. Нахождение процентного отношения двух чисел (задачи)
- Урок 10. Простые и сложные проценты
- Урок 11. Задачи на время
- Урок 12. Задачи на нахождение чисел по их сумме или разности
- Урок 13. Задачи на нахождение чисел по их сумме или разности и отношению
- Урок 14. Среднее арифметическое
- Урок 15. Среднее арифметическое (задачи)
- Урок 16. Масштаб карты или чертежа
- Урок 17. Определение расстояния на местности и действительных размеров предметов с помощью масштаба
- Урок 18. Определение расстояния на карте или чертеже с помощью масштаба
- Урок 19. Задачи на встречное движение
- Урок 20. Задачи на движение в одном направлении
- Урок 21. Задачи на движение в противоположных направлениях
- Урок 22. Задачи на движение по реке
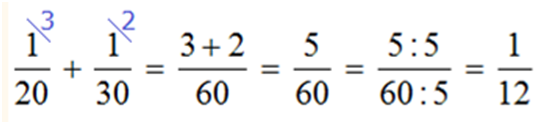






Комментариев нет:
Отправить комментарий