ВИДЕОУРОК
ЗАДАЧА:
Если две величины связаны между собой так, что при
увеличении (уменьшении) значения одного из них в несколько раз значение второй увеличивается (уменьшается) во столько же раз, то такие величины называются прямо
пропорциональными.
Такие величины
говорят также, что они связаны между собой прямо пропорциональной зависимостью.
В природе и в окружающей жизни встречается много таких величин.
ПРИМЕР:
у/х = k
следует, что
y = kx.
Наоборот, если зависимость переменной у от переменной х выражается формулой y = kx, где k – не равное нулю число, то отношение у/х (при х ≠ 0) постоянно: у/х = k, т. е. переменная у пропорциональна переменной х.
ПРИМЕР:
6 : 2 = 3;
120 : 40 = 3.
Почему это так ? А потому, что эти величины прямо
пропорциональны, то есть, когда одна из них увеличилась в 20
раз, то и вторая увеличилась в 20 раз.
Итак, мы пришли к
такому выводу: если взять два каких-либо значения первой величины и разделить
их друг на друга, а затем разделить одно на одно соответствующие им значения
второй величины, то в обоих случаях получим одно и то же число, то есть одно и
то же отношение. Значит, два отношения, которые мы выше писали, можно соединить
знаком равенства, то есть
6 : 2 = 120 : 40.
Нет сомнения в том,
что если бы мы взяли не эти отношения, а другие и не в том порядке, а в
обратном, то также получили равенство отношений. Действительно, будем
рассматривать значение наших величин слева направо:
2 : 6 = 1/3;
40 : 120 = 1/3.
Итак, мы можем написать:
2 : 6 = 40 : 120.
12 килограммов кокса заменяют 20
килограммов каменного угля. Сколько килограммов каменного угля заменят 210
килограммов кокса ?
РЕШЕНИЕ:
Если 12 кг кокса
заменяют 20
кг угля, то пусть 210
кг кокса заменяют х
кг угля. Составим пропорцию:
12 кг –––– 20 кг угля;
210 кг
–––– х кг угля.
Или: 12
кг кокса так относятся к 20
кг угля, как 210
кг кокса относятся к х
кг угля:
12 : 20 = 210 : х.
ОТВЕТ: 350 кг
ЗАДАЧА:
Пекарь за 8 часов испёк 70 булочек. Сколько булочек он испечёт за 12
часов ?
РЕШЕНИЕ:
Если 70 булочек пекарь печёт
8
часов, то пусть х булочек он испечёт за
12
часов. Составим пропорцию:
70 булочек
–––– 8 часов;
х булочек –––– 12 часов.
Или: 70
булочек так
относятся к 8 часам, как х булочек относятся
к 12
часам:
70 : 8 = х : 12.
ОТВЕТ: 105 булочек
ЗАДАЧА:
За 8 часов трактор вспахал
0,6 га.
За сколько часов он вспашет 4,2 га ?
РЕШЕНИЕ:
Если за 8 часов трактор вспахал
0,6 га,
то за х
часов трактор вспашет 4,2 га. Составим пропорцию:
8 часов
–––– 0,6 га;
х часов –––– 4,2 га.
Или: 8 часов так относятся к 0,6 га, как х часов относятся
к 4,2
га:
8 : 0,6 = х : 4,2.
ОТВЕТ: 56 часов
ЗАДАЧА:
На 20 гектарах пашни было посеяно 3,4
т овса. Сколько
зерна потребуется для засева 1980 гектаров пашни ?
РЕШЕНИЕ:
Если на 20 гектарах пашни было посеяно 3,4
т овса, то х
т овса надо чтобы засеять 1980
гектаров пашни. Составим пропорцию:
3,4 т
–––– 20 га;
х т –––– 1980 га.
Или: 3,4 т так
относятся к 20 га, как х т относятся к 1980 га:
3,4 : 20 = х : 1980.
ОТВЕТ: 336,6 т
ЗАДАЧА:
Токарь за 8 часов изготовил 70 деталей. Сколько деталей он изготовит за 12
часов ?
РЕШЕНИЕ:
Если 70 деталей токарь изготовит за 8
часов, то пусть х деталей он изготовит за
12
часов. Составим пропорцию:
70 деталей
–––– 8 часов;
х деталей –––– 12 часов.
Или: 70
деталей так
относятся к 8 часам, как х деталей относятся
к 12
часам:
70 : 8 = х : 12.
Для решения многих
типовых задач существуют специальные правила их решения. Задачи на прямую и
обратную пропорциональность, в которых по трём значениям двух величин нужно
найти четвёртое, называются задачами на тройное правило.
Если же для трёх
величин, были даны пять значений, и требовалось найти шестое, то правило
называется пятерным.
Аналогично для четырёх величин существовало семеричное правило.
Задачи, в которых
по данному ряду соответствующих друг другу значений нескольких (более двух)
пропорциональных величин требуется найти значение одной из них, соответствующее
другому ряду данных значений остальных величин, называют задачами на сложное тройное
правило.
Сложное тройное правило применяется при решении задач, в которых участвует n (n ˃ 2) величин
x1, x2,…, хn – 1, хn.
В этом случае
у n – 1 величин x1, x2,…, хn – 1 известны по два значения a1, a2, b1, b2, …, l1, l2, а
у хn известно только
одно значение k1,
другое – k2 подлежит
определению.
Практически сложное тройное
правило представляет собой последовательное применение простого
тройного правила.
Чтобы получить искомое число, достаточно данное
значение той же величины умножить последовательно на отношения данных значений
остальных величин, беря отношение нового значения к прежнему, если величина
прямо пропорциональна той, значение которой отыскивается, и прежнего значения к
новому, когда величина обратно пропорциональна той, значение которой
отыскивается.
ЗАДАЧА:
5 насосов в течение
3 час выкачали 1800 вёдер воды. Сколько воды выкачивают 4 таких насоса в течение 4 час ?
РЕШЕНИЕ:
1 способ.
Сначала найдём, сколько вёдер воды выкачал 1 насос в течение 3
час.
1800 : 5 = 360 (вёдер).
Затем найдём, сколько вёдер воды выкачал 1 насос в течение 1
часа.
3600 : 3 = 120 (вёдер).
Теперь определим, сколько воды выкачивают 4 насоса за
1 час.
120 ∙ 4 = 480 (вёдер).
А теперь определим, сколько воды выкачивают 4 насоса за
4 часа.
480 ∙ 4 = 1920 (вёдер).
2 способ.
Составим пропорцию:
5 нас.
3 час ---------- 1800 вёд.
4 нас. 4 час ---------- х вёд.
За 18 рабочих дней бригада лесорубов в составе 15 человек
заготовила 972 м3 дров. Сколько дров заготовят 12 человек
за 25
дней при такой же самой производительности труда ?
РЕШЕНИЕ:
1 способ .
Приведение к единице.
Этот способ связан с введением человеко-дня и приведением
к единице.
Сколько человеко-дней затрачено, чтобы заготовить 972 м3 дров ?
15 ∙ 18 = 270.
12 ∙ 25 = 300.
Эту задачу можно привести до задачи на простое тройное
правило, которую можно решить с помощью пропорций. Это можно осуществить, решив
предварительно первый и третий вопрос по предыдущему способу:
270 ----- 972
Укороченная запись:
18 ----- 15
----- 972
25 ----- 12
----- х
Решения и объяснения.
х1 = 972 м3
Если 15 человек работали 18 дней.
Объяснение решения
2
способом имело б такой вид:
Первая бригада на заготовку 972 м3 дров затратила
15 ∙ 18 = 270 человеко-дней.
12 ∙ 25 = 300 человеко-дни.
- Урок 1. Отношение величин
- Урок 2. Пропорции
- Урок 4. Величины обратно пропорциональные
- Урок 5. Пропорциональное деление
- Урок 6. Проценты
- Урок 7. Нахождение процентов данного числа (задачи)
- Урок 8. Нахождение числа по его процентам (задачи)
- Урок 9. Нахождение процентного отношения двух чисел (задачи)
- Урок 10. Простые и сложные проценты
- Урок 11. Задачи на время
- Урок 12. Задачи на нахождение чисел по их сумме или разности
- Урок 13. Задачи на нахождение чисел по их сумме или разности и отношению
- Урок 14. Среднее арифметическое
- Урок 15. Среднее арифметическое (задачи)
- Урок 16. Масштаб карты или чертежа
- Урок 17. Определение расстояния на местности и действительных размеров предметов с помощью масштаба
- Урок 18. Определение расстояния на карте или чертеже с помощью масштаба
- Урок 19. Задачи на встречное движение
- Урок 20. Задачи на движение в одном направлении
- Урок 21. Задачи на движение в противоположных направлениях
- Урок 22. Задачи на движение по реке
- Урок 23. Задачи на совместную работу




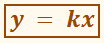













Комментариев нет:
Отправить комментарий