Уроки математики и физики (RU + UA)

▼

вторник, 30 мая 2017 г.

Урок 10. Нахождение области определения и области значения функции с помощью графика

Если функция задана графически, то для нахождения области определения её график надо спроектировать на ось  Ох. А если график функции спроектировать на ось  Оу, получим область изменения (значения) функции.
Нахождение области значений функции по её графику.

Постройте график функции. Во многих случаях проще найти область значений функции, построив её график.
Областью значений многих квадратичных функций является

(–∞, 0]  или  [0, ∞),

так как вершина параболы, направленной вправо или влево, лежит на оси  Х. В этом случае область значений включает все положительные значения  у, если парабола возрастает, или все отрицательные значения  у, если парабола убывает.
Вершины графиков некоторых функций лежат выше или ниже оси  Х. в этом случае область значений определяется координатой  у  вершины параболы.

ПРИМЕР:

Если координата  у  вершины параболы равна  –4, а парабола возрастает, то область значений равна

[–4, ∞).

Построив график функции, вы увидите на нём точку, в которой функция имеет минимальное значение. Если наглядного минимума нет, он не существует, а график функции уходит в бесконечность.
Построив график функции, вы увидите на нём точку, в которой функция имеет максимальное значение. Если наглядного максимума нет, он не существует, а график функции уходит в бесконечность.
Самый простой способ построить график функции – это воспользоваться графическим калькулятором или специальным программным обеспечением. Если нет графического калькулятора, постройте приблизительный график, подставив в функцию несколько значений  х  и, вычислив соответствующие значения  у, нанесите найденные точки на координатную плоскость, чтобы получить общее представление о форме графика.

ПРИМЕР:

Найдите область значений функции  у = √͞͞͞͞͞x  по графику.
РЕШЕНИЕ:

Из графика видно, что минимальное значение переменная  у  принимает при  х = 0. Максимальное значение не определяется, при этом видно, что при возрастании  х  значение  у  также растёт. Тогда область значений будет следующая:

Е(у) = [0; +∞).

Ниже приведены несколько примеров графиков функций.

Графики функций показаны жирными синими линиями, тонкие красные линии – это асимптоты, жёлтыми точками и линиями на оси  0у  изображена область значений соответствующей функции.

Тёмные точки обозначают, что число входит в область значений.

Светлые точки обозначают, что число не входит в область значений.

ПРИМЕР:

Найдите область определения и область значения функции  у = 2,6  по графику.
РЕШЕНИЕ:

Из графика видно, что функцией является прямая, которая параллельна оси  х  и пересекает ось  у  в точке  2,6. Прямая стремится в бесконечность и  вправо и влево вдоль параллельно оси  х, не пересекая её, а также пересекает ось  у  в точке  у = 2,6 (на графике тёмная точка), значит область определения будет

D(у) = (–∞; +∞).

Область значения очевидна:

Е(у) = {2,6}.

ПРИМЕР:

Найдите область определения и область значения функции по графику.
РЕШЕНИЕ:

Из графика видно, что функция стремится в бесконечность и  вправо и влево вдоль оси  х, не пересекая её (на графике белая точка), а также пересекает ось  у  в точке  у = 9 (на графике тёмная точка),  значит область определения будет

D(у) = (–∞; +∞).

Область значения очевидна:

Е(у) = (0; 9].

Ноль не входит в область значений, а девять входит.

ПРИМЕР:

Найдите область определения и область значения функции
по графику.
РЕШЕНИЕ:

Из графика видно, что функцией является кривая, которая пересекает ось  у  в точке  0. Кривая стремится в бесконечность и  вправо и влево, максимум которой  +1, а минимум –1 (на графике тёмные точки), значит область определения будет

D(у) = (–∞; +∞).

Область значения очевидна:

Е(у) = [+1; –1].

ПРИМЕР:

Найдите область определения и область значения функции

у = arctg x

по графику.
РЕШЕНИЕ:

Из графика видно, что функцией является кривая, которая пересекает ось  у  в точке  0. Кривая стремится в бесконечность и  вправо и влево. Стремится к точкам  + π/2  и  – π/2 (на графике светлые точки), значит область определения будет

D(у) = (–∞; +∞).

Область значения очевидна:

Е(у) = (–π/2; + π/2).

ПРИМЕР:

Найдите область определения и область значения функции

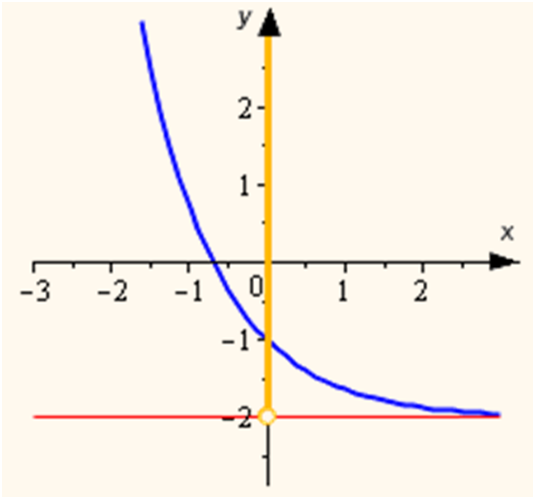
у = е–х – 2

по графику.
РЕШЕНИЕ:

Из графика видно, что функцией является кривая, которая пересекает ось  у  в точке  –1. Кривая стремится в бесконечность и  вправо и влево. Стремится к точке   –2  (на графике светлая точка), значит область определения будет

D(у) = (–∞; +∞).

Область значения очевидна:

Е(у) = (–2; +∞).

ПРИМЕР:

Найдите область определения и область значения функции
по графику.

 РЕШЕНИЕ:

Из графика видно, что функцией являются две кривые, одна из которых пересекает ось  у  в точке  0. Кривые стремится в бесконечность и  вправо и влево, а также стремятся к асимптоте  х = 2, значит область определения будет

D(у) = (–∞; 2) ∪ (2; +∞).

Область значения очевидна:

Е(у) = (–∞; 0] ∪ [4; +∞).

ПРИМЕР:

Найдите область определения и область значения функции
по графику.
РЕШЕНИЕ:

Из графика видно, что функцией являются две кривые, одна из которых пересекает ось  у  в точке  0. Кривые стремится в бесконечность и  вправо и влево, а также стремятся к асимптотам  х = 2  и  у = 1, значит область определения будет

D(у) = (–∞; 2) ∪ (2; +∞).

Область значения очевидна:

Е(у) = (–∞; 1) ∪ (1; +∞).

ПРИМЕР:

Найдите область значения функции
по графику.
РЕШЕНИЕ:

Область значения очевидна:

Е(у) = [–6; –2] ∪ {–1} ∪ (0; +∞).

ПРИМЕР:

Найдите область значения функции
по графику.
РЕШЕНИЕ:

Область значения очевидна:

Е(у) = (–2е; +∞).

Задания к уроку 10
Другие уроки:
на

Комментариев нет:

Отправить комментарий