ПРИМЕР:
Получим другое отношение – отношение q между элементами множества Y и элементами множества Х.
Говорят, что q есть отношение, обратное отношению р. В свою очередь отношение р является обратным отношению q.
Областью определения отношения p является множество
{–3; –2; –1},
а областью значений – множество
{2; 3; 4; 5}
Для отношения q, обратного отношению р, областью определения служит множество
{2; 3; 4; 5},
а областью значений – множество
{–3; –2; –1}.
Таким образом, область определения и область значений взаимно-обратных отношений меняются ролями.
Отношение p между элементами множеств Х и Y определяется множеством пар:
{(–3; 2); (–2; 3); (–1; 4); (–1; 5)}
Поменяв в каждой паре местами её элементы, получим множество пар, которым задаётся отношение q, обратное р:
{(2; –3); (3; –2); (4; –1); (5; –1)}
Если отношение определяется некоторым множеством пар, то обратное ему отношение определяется множеством пар, которое получено из первого перестановкой элементов в каждой паре.
ПРИМЕР:
Вернёмся к рассмотренным выше взаимно-обратным отношениям р и q.
Построим теперь графики отношений р и q в одной и той же системе координат.
Нетрудно заметить, что точки с координатами
(–3; 2) и (2; –3), (–1; 4) и (4; –1) и т. д.,
т. е. точки, у которых абсцисса первой является ординатой второй и ордината первой является абсциссой второй, симметричны относительно прямой
у = х.
Каждой точке графика отношения р соответствует симметричная относительно прямой у = х точка графика отношения q, и наоборот, каждой точке графика отношения q соответствует симметричная относительно прямой у = х точка графика отношения р. Поэтому графики отношений р и q симметричны относительно прямой у = х.
Вообще справедлива следующая теорема:
Графики взаимно-обратных отношений между числами симметричны относительно прямой у = х.
Приведём примеры взаимно-обратных отношений
ПРИМЕР:
На рисунке с помощью стрелок показано отношение <<меньше>> между элементами множества
А = {5; 7; 10}
ПРИМЕР:
Отношение <<быть делителем>> и <<быть кратным>> между натуральными числами – взаимно-обратные отношения.
Понятие о функции, обратной данной.
Если функция у = f(х) такова, что для любого её
значения у0 уравнение f(х) = у0 имеет
относительно х единственный
корень, то говорят, что функция у = f(х) обратима.
Если функция у = f(х) обратима, то, выразив х их формулы у =
f(х) и поменяв затем х и у местами, получим
обратную функцию, её обозначают
у = f -1 (х).
На рисунку с помощью стрелок задано отношение р между элементами множеств А и В. Это отношение – функция, так как каждому элементу множества А соответствует не более одного множества В.
Отношение q между элементами множества В и А, обратное р, не является функцией: в множестве В существует элемент (число 2), которому соответствует более одного элемента из множества А (элементы 5 и 6).
ПРИМЕР:
На рисунках с помощью стрелок задано отношение f между элементами множеств X и Y и обратное ему отношение g между элементами множеств Y и X.
Отношение f – функция, отношение g, обратное f, тоже функция.
Приведённые примеры показывают, что отношение, обратное функции, может быть функцией, а может и не быть функцией.
Функция f называется обратимой, если обратное ей отношение – функция.
В этом случае отношение, обратное функции f, называют функцией, обратной f.
Функция обратима тогда и только тогда, когда каждое своё значение она принимает лишь при одном значении аргумента.
Если
функция у = f(х) определена и возрастает (убывает) на промежутке Х и областью её значений является
промежуток Y,
то у неё существует обратная функция, причём обратная функция определена и
возрастает (убывает) на Y.
Для нахождения функции, обратной данной
у = f(х), надо выразить х через у: х = g(у), а затем записать полученную функцию в общепринятой форме у = g(х).
Если функции у = f(х) и у = g(х) являются взаимно обратными, то область
определения функции f совпадает с множеством значений функции g и, наоборот,
область определения функции g совпадает с множеством значений функции f, то есть
D(f) =
E(g) и D(g) =
E(f).
Всякая
возрастающая функция обратима.
Функция,
обратная возрастающей, является возрастающей.
Всякая убывающая
функция обратима.
Функция,
обратная убывающей, является убывающей.
Если некоторое
отношение f задано уравнением с двумя переменными х и у,
то для задания уравнением отношения, обратного
f,
достаточно в данном уравнении поменять обозначения х на у и у на х.
ПРИМЕР:
Функция f,
заданная формулой
у = –2х + 3,
убывающая. Поэтому она
обратима. Обратная ей функция также убывающая.
Чтобы задать формулой функцию,
обратную f,
поменяем в уравнении
у = –2х + 3,
обозначения х на у и у на х. Получим
уравнение
х = –2у + 3,
Обычно при задании функции
уравнением с переменными х и у переменную
у выражают через
переменную х.
В данном случае имеем:
2у = –х + 3,
у = –0,5х + 1,5.
Мы получили формулу, которой
задаётся функция, обратная f.
ПРИМЕР:
Пусть дана функция:
у = 3х – 2.
Эта функция, обратная данной. Данную функцию также можно назвать обратной по отношению к полученной. Эти функции взаимно обратные.
ПРИМЕР:
Для функции, заданной равенством:
у = х2
На
(–∞; +∞ ),
обратной не существует. А для
функции:
у = х2
заданной на промежутке
[0; +∞),
обратная функция существует.
Найдите
функцию,
обратную
данной
функции
у
= 1/6 х – 7.
РЕШЕНИЕ:
у = 1/6 х – 7,
6у = х – 42,
х = 6у + 42.
Обратной
будет
функция
у = 6х + 42.
ПРИМЕР:
Найдите
функцию,
обратную
данной
функции
у
= 1/3 х + 2.
РЕШЕНИЕ:
у = 1/3 х + 2,
3у = х + 6,
х
= 3у – 6.
Обратной
будет
функция
у = 3х – 6.
ПРИМЕР:
Найдите функцию, обратную данной функции
РЕШЕНИЕ:Обратной будет функцияПРИМЕР:На рисунках изображены графики функций g и h.
Функция g обратима, так как нет такого значения функции, которое соответствовало бы различным значениям аргумента (любая прямая, параллельная оси х, пересекает график не более чем в одной точке).
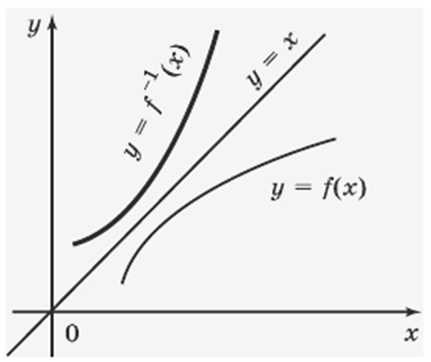
Если точка (х; у) принадлежит
графику функции у = f(х), то точка (у; х) принадлежит
графику обратной функции. Поэтому график обратной функции получается из графика
функции у = f(х) с помощью преобразования плоскости ху, переводящего точки
(у; х) в точки
(х; у). Этим
преобразованием является преобразование осевой симметрии относительно
прямой у = х (ось симметрии).
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 23. График функции обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований






















Комментариев нет:
Отправить комментарий