дріб m/n дорівнює нулю тоді і тільки тоді, коли його чисельник дорівнює нулю, а
знаменник відмінний від нуля (на 0 ділити не можна).
Записується це так:
m
= 0, n ≠
0.
Якщо q(x) ≠ 0, то знайдений корінь рівняння р(х) = 0 є і коренем рівнянняЯкщо q(x) = 0, то отриманий корінь рівняння р(х) = 0 не є коренем рівнянняТаким чином, рівняння р(х) = 0 є наслідком рівнянняПри переході від рівняннядо рівняння р(х) = 0 (звільнення від знаменника) можуть виникнути сторонні коріння. Відсіяти їх можна за допомогою умови q(x) ≠ 0 (або за допомогою безпосередньої підстановки кожного кореня рівняння р(х) = 0 в рівнянняОбласть визначення рівняння (ОДЗ).
Областю визначення
рівняння f(х) = q(x) називають безліч тих значень змінної х, у яких вирази f(х) і q(x) мають сенс (одночасно).
ПРИКЛАД:
Знайти
область визначення рівняння:
х2
– 5х = 1 + 2х.
РОЗВ'ЯЗАННЯ:
Вирази
х2 – 5х і 1 + 2х визначені
за всіх х.
Отже, область визначення рівняння – вся числова пряма.
ПРИКЛАД:
ПРИКЛАД:
Корінь
парного ступеня має сенс лише за невід'ємних значеннях підкореного
висловлювання. Отже, одночасно мають виконуватися умови:
х
≥ 0, х – 1 ≥ 0, х – 2 ≥ 0.
Всі
ці нерівності справедливі за х
≥ 2, тобто
[2; +∞) – область визначення рівняння.
Замість терміна
<<область визначення рівняння>> часто використовують термін
<<область допустимих значень>> змінної (ОДЗ).
Зрозуміло, що коріння
рівняння f(х) = q(x) має належати його області визначення (його ОДЗ). Але іноді буває отже у процесі
перетворень рівняння його область визначення змінюється (найчастіше вона
розширюється) і знайдених значень змінної одні належать області визначення
рівняння f(х) = q(x), інші ж не належать.
Тоді перші є корінням рівняння, а другі – ні (це сторонні корені).
Загальний висновок
такий:
якщо в процесі перетворення рівняння
його область визначення розширилася, то можуть виникнути сторонні корені.
Тому всі знайдені
значення змінної треба перевірити підстановкою у вихідне рівняння або за
допомогою області визначення (ОДЗ)
вихідного рівняння.
Алгоритм розв'язання
рівняння, що містить змінну у знаменнику.
– перенести всі елементи з правої
частини рівняння до лівої частини;
– для отримання тотожного рівняння
необхідно змінити всі знаки, що стоять перед виразами у правій частині
протилежні;
– якщо в лівій частині вийде вираз
із різними знаменниками, то їх треба привести до спільного знаменника,
використовуючи основну властивість дробу;
– виконати перетворення,
використовуючи тотожні перетворення і отримати підсумковий дріб, що дорівнює 0;
– прирівняти чисельник до 0 і знайти коріння рівняння, що вийшло;
– провести вибірку коренів, тобто знайти
допустимі значення змінних, які не звертають знаменник в 0.
ПРИКЛАД:
(2х – 1)(х + 3).
(2х + 3)(х + 3) =
=
2х ∙ х + 2х ∙ 3 + 3 ∙ х + 3 ∙ 3 =
=
2х2 + 6х + 3х
+ 9 = 2х2 + 9х + 9.
Виконаємо аналогічні перетворення в
чисельнику другого дробу:
(х – 5)(2х – 1) =
=
х ∙ 2х – х ∙ 1 – 5 ∙ 2х + 5 ∙ 1 =
=
2х2 – х – 10х + 5 = 2х2 – 11х + 5.
20х + 4 = 0.
Розв'яжемо
лінійне рівняння:
20х = –4,
х = –0,2.
Проведемо
вибірку коріння. Це означає, що необхідно перевірити, чи не звертаються
знаменники вихідних дробів в 0 при знайденому корінні.
Поставимо
умову, що знаменники не дорівнюють 0.
2х – 1 ≠ 0, х ≠
0,5.
х
+ 3 ≠ 0. х ≠ –3.
значить
допустимі значення змінних, крім –3 і 0,5.
Знайдений
корінь є допустимим значенням, отже, він є коренем рівняння. Якби знайдений
корінь був би не допустимим значенням, то такий корінь був би стороннім і,
звичайно, не був би включений у відповідь.
ВІДПОВІДЬ: –0,2
Використання основної
властивості пропорції під час вирішення рівнянь.
Основною властивістю
пропорції і те, що добуток крайніх членів пропорції дорівнює добутку середніх
членів.
Використовуємо цю
властивість для вирішення попереднього рішення.
ПРИКЛАД:
Знайдемо
та прирівняємо добуток крайніх та середніх членів пропорції:
(2х + 3) ∙
(х + 3) = (х – 5) ∙ (2х – 1),
2х2 + 6х + 3х + 9 = 2х2 – х – 10х + 5,
9х +
11х = 5 – 9, 20х
= –4, х = –0,2.
З
попереднього рішення ми виявили, що допустимі будь-які значення, крім –3
і 0,5.
Тоді, встановивши, що знайдений корінь є допустимим значенням, з'ясували, що –0,2 буде коренем.
ВІДПОВІДЬ: –0,2
ПРИКЛАД:
Зведемо вирази в левій і правій частинах його спільного знаменника:
Оскільки знаменники цих дробів однакові, то дроби будуть рівні при тих і тільки тих значеннях х, при яких чисельники рівні між собою і знаменник відмінний від нуля, тобто рівність справджується тоді і тільки тоді, коли виконується умова:
і замінимо вираз у лівій частині дробом:
Використавши умову рівності дробу нулю, маємо:
у + 1 + 4у – 12 = 4;
дріб дорівнює нулю
тільки тоді, коли чисельник дорівнює нулю, а знаменник відмінний від нуля.
Прирівняємо
чисельник до нуля:
8х – 4 =
0, 8х
= 4, х
= 0,5.
Якщо х
= 0,5, знаменник х2 – 4 не дорівнює
0.
Тому,
х = 0,5 – корінь даного рівняння.
ПРИКЛАД:
якщо х
= 0 або х
= 2.
Коли х
= 0, знаменник
(х – 2)(х + 3)
не
дорівнює 0. Тому,
х
= 0 – корінь цього
рівняння.
Коли х
= 2, то
(х – 2)(х + 3) = 0.
Тому,
х = 2 – не буде коренем даного рівняння.
ВІДПОВІДЬ: х = 0.
ПРИКЛАД:
Завдання до уроку 6
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 2. Лінійне рівняння з одним невідомим і дрібними вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 14. Рішення лінійних систем рівнянь за допомогою графіків
- Урок 15. Розв'язування задач за допомогою систем лінійних рівнянь
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 22. Графічний спосіб розв'язування квадратних рівнянь
- Урок 23. Квадратний тричлен
- Урок 24. Квадратні рівняння з параметрами
- Урок 25. Дробові раціональні рівняння
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння













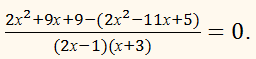
















Комментариев нет:
Отправить комментарий