Уроки математики и физики (RU + UA)

▼

среда, 1 февраля 2017 г.

Урок 37. Задачі на знаходження цифр

Основні відомості про десяткову систему числення.

ПРИКЛАД:

327  = 100 × 3 + 2 × 10 + 7.

Водночас доцільно ввести й позначення:
ЗАДАЧА:

Двоцифрове число закінчується цифрою  3. Якщо це число додати до числа, записаного тими самими цифрами, але в зворотному порядку, то буде  55. Знайдіть двоцифрове число.
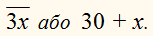
Двоцифрове число, яке закінчується цифрою  3, можна позначити так
Число, записане цими самими цифрами, але в зворотному порядку, буде:
Сума цих двох чисел дорівнює  55, отже,

(10х + 3) + (30 + х) = 55,
х = 2.

ВІДПОВІДЬ:

Двоцифрове число буде  23.

ЗАДАЧА:

Сума цифр двоцифрового числа  15. Якщо це число помножити на  7  і від добутку відняти двоцифрове число, записане тими самими цифрами, що і початкове, але в зворотному порядку, то дістанемо  387. Знайдіть двоцифрове число.
Позначимо цифру десятків через  х, а цифру одиниць – через  у. Оскільки сума цих цифр дорівнює  15, маємо рівняння 

х + у = 15.

Крім того, з умови задачі випливає ще одне рівняння: 

(10х + у) × 7 – (10у + х) = 387, або 
23х – у = 129.

Система рівнянь:
х = 6,  у = 9.

ВІДПОВІДЬ:

Двоцифрове число буде  69.

ЗАДАЧА:

На нумерацію сторінок книги знадобилося в два рази більше цифр, ніж сторінок. Скільки сторінок в книзі ?

РІШЕННЯ:

Спосіб 1. На перші  9  сторінок знадобиться  9  цифр. Якщо в книзі менше  100  сторінок, то, починаючи з десятої сторінки, номера сторінок – двозначні числа. Нехай в книзі   (х + 9)   сторінок, тоді для нумерації знадобиться   (2х + 9)   цифр. А по умові завдання для нумерації вимагається  2(х + 9) цифр. Складемо рівняння:

2х + 9 = 2х + 18.

Це рівняння не має рішень, означає в книзі більше  99  сторінок. Якщо в книзі менше  1000  сторінок, то, починаючи з сотої сторінки, номера сторінок – тризначні. Нехай в книзі 

(9 + 90 + у)  сторінок

тоді для нумерації сторінок знадобиться 

(9 + 2 × 90 + 3у)  цифр.

А по умові завдання потрібне для нумерації число цифр 

2(у + 99).

Складемо рівняння:

3у + 180 + 9 = 2у + 198.

Вирішивши це рівняння, отримаємо  у = 9. В книзі  (99 + 9) сторінок, т. е.  108  сторінок.
Переконайтеся, що якщо число сторінок в книзі більше  999, то число цифр, необхідних для їх нумерації, перевершує число сторінок більш ніж в  2  рази. Таким чином інших рішень немає.

ВІДПОВІДЬ:

108  сторінок.

Спосіб 2. Очевидно, що якщо брати для нумерації сторінок тільки однозначні і двозначні числа, то кількість цифр не може удвічі перевершувати кількість чисел. Від  10  до  99 –  кількість цифр удвічі перевершує кількість чисел. Від  1  до  9  бракує  9  цифр, значить, треба використати ще  9  тризначних чисел (від  100  до  108). Таким чином, в книзі  108  сторінок.  

 Завдання до уроку 37
Інші уроки:
на

Комментариев нет:

Отправить комментарий