Властивості
ступеня цілого позитивного числа із позитивним показником.
Степінь будь-якого цілого позитивного числа з
позитивним показником визначається так само, як і ступінь натурального числа,
тобто є добуток кількох рівних співмножників.
ПРИКЛАД:
22
∙ 23 = 22+3 = 25 = 32,
42
∙ 45 = 42+5 = 47,
аm
× аn = am+n
називають основною властивістю степеня. З неї
випливає, що:
Яке б не було ціле число a і натуральні показники степенів m і n, завжди:
ПРИКЛАД:
(33)4
= 33∙4 =
312,
(24)3
= 24∙3 =
212.
Для будь-яких цілих чисел а і b і натурального показника степеня n:
ПРИКЛАД:
(5
∙ 4)4 =
54 ∙ 44,
32
× 35 =
37,
Завдання до уроку 8
Інші уроки:
- Урок 1. Цілі числа
- Урок 2. Абсолютна величина числа
- Урок 3. Додавання цілих чисел
- Урок 4. Віднімання цілих чисел
- Урок 5. Множення цілих чисел
- Урок 6. Ділення цілих чисел
- Урок 7. Обчислення величини виразів, які стоять під знаком абсолютної величини
- Урок 9. Степінь цілого відмінного числа з натуральним показником
- Урок 10. Степінь цілого додатного числа з цілим показником
- Урок 11. Степінь цілого відмінного числа з цілим показником
- Урок 12. Ділення степенів цілих чисел з натуральним показником
- Урок 13. Ділення степенів цілих чисел з цілим показником
- Урок 14. Стандартний вигляд числа
- Урок 15. Раціональні числа
- Урок 16. Додавання раціональних чисел
- Урок 17. Віднімання раціональних чисел
- Урок 18. Множення раціональних чисел
- Урок 19. Ділення раціональних чисел
- Урок 20. Нескінченні періодичні десяткові дроби
- Урок 21.Степінь раціонального додатного числа з натуральним показником
- Урок 22. Степінь раціонального відмінного числа з натуральним показником
- Урок 23. Степінь раціонального додатного числа з цілим показником
- Урок 24. Степінь раціонального відмінного числа з цілим показником
- Урок 25. Ділення степенів раціональних чисел з цілим показником


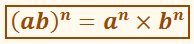
Комментариев нет:
Отправить комментарий