Будь-яке
раціональне число можна представити у вигляді нескінченного періодичного
десяткового дробу. Кожен нескінченний періодичний десятковий дріб представляє
деяке раціональне число. При перетворенні звичайних дробів на десяткові часто
отримуємо нескінченні періодичні дроби.
Звернення звичайного дробу до
нескінченного десяткового періодичного дробу.
Нехай дано
десятковий дріб 2,73.
Її значення не зміниться, якщо праворуч приписати будь-яку кількість нулів
2,73 = 2,730 = 2,7300 = … = 2,73000 … 0.
Будь-який звичайний дріб можна подати у вигляді
нескінченного десяткового дробу.
ПРИКЛАД:
Візьмемо дріб 3/14 і ділитимемо чисельник на знаменник,
поступово отримуючи десяткові знаки. При цьому зауважимо, що будь-яке
натуральне число можна представити як нескінченний десятковий дріб.
3 = 3,000 …
3/14 = 0,214285714 … .
Випишемо послідовно залишки, які вийшли під час виконання
операції поділу:
2, 6, 4, 12, 8, 10, 2, 6, … .
Зрозуміло, що всі ці залишки менші від дільника, тобто
менше числа 14. Це означає, що на якомусь кроці поділу має неминуче
знову з'явитися такий залишок, який уже зустрічався раніше. Так, на сьомому
етапі з'явився залишок 2, який був на першому етапі. Зрозуміло, що як тільки
з'явиться залишок, який вже зустрічався, за ним підуть залишки у тій самій
послідовності, що була раніше. У нашому прикладі за залишком 2 йде залишок 6,
за ним 4,
за ним 12 і
так далі, тобто отримуємо таку послідовність залишків:
2, 6, 4, 12, 8, 10, 2, 6, 4, 12, 8, 10, … .
Групи залишків, що періодично повторюються, приведуть
відповідно до періодично повторюваної групи цифр у десятковому записі числа.
Так, у нашому прикладі отримаємо:
3/14 = 0,2142857142857142857 … .
Послідовно повторювану групу цифр (мінімальну) після коми в десятковому записі числа називають періодом, а
нескінченний десятковий дріб, що має такий період у своєму записі, називають
періодичним.
Для стислості прийнято період записувати один раз,
укладаючи його в круглі дужки:
0,2142857142857142857 … = 0,2 (142857).
Якщо період починається відразу після коми, то дріб
називають чистим періодичним, якщо ж між комою і періодом є інші десяткові
знаки, то дріб називають змішаним періодичним.
ПРИКЛАД:
2,(23) = 2,2323232323 … – чистий періодичний дріб,
0,2,(142857) – змішаний періодичний дріб,
2,73 = 2,73000 … = 2,73 (0) – змішаний періодичний дріб.
ПРИКЛАД:
2/3 = 2 : 3 = 0,66... ;
5/6 = 5 : 6 = 0,833... ;
3/11 = 3 : 11 = 0,2727... .
Дріб 0,66...
називається нескінченним періодичним десятковим дробом, період якого є число 6.
Дріб 0,833… теж періодична, але її період (число 3) починається не
відразу після коми.
Дріб 0,2727… періодична, періодом якої буде число 27.
Періодичні дроби ще записуються так:
0,66... = 0,(6),
а вимовляються так:
0 цілих та 6 у періоді;
0,833… = 0,8(3)
(0 цілих 8 десятих та 3 у періоді);
0,2727… = 0,(27)
(0 цілих 27 у періоді).
Якщо при
розкладанні знаменника нескоротного дробу на прості множники, крім чисел 2 і 5, є інші прості числа, то такий дріб перетворюється на
нескінченний періодичний дріб.
Яке
з даних чисел не можна записати у вигляді скінченного десяткового дробу
?
3/15, 1/7, 1/8, 13/250.
Звернення нескінченного
десяткового періодичного дробу в звичайний дріб.
Щоб нескінченний
десятковий дріб помножити на 10, 100, 1000 і так далі, достатньо, як і в кінцевому десятковому
дробі, перенести ком на один, два, три і так далі знака вправо.
ПРИКЛАД:
0,1(23) ∙ 100 = 0,1232323 … ∙ 100 =
= 12,323232 … = 12,(32).
Звернення періодичного
десяткового дробу в звичайний дріб розглянемо на прикладах.
ПРИКЛАД:
Звернути у звичайний дріб число:
0,(13).
РОЗВ'ЯЗАННЯ:
Покладемо
х = 0,(13) = 0,131313 … .
Помножимо чистий періодичний дріб х на таке число, щоб
кома перемістилася рівно на період праворуч. Оскільки в періоді дві цифри,
треба перенести кому на дві цифри вправо, а для цього достатньо помножити число
х на 100,
тоді
100х = 0,131313 … ∙ 100 = 13,1313 … = 13,(13).
Тепер віднімемо х із 100х:
100х – х = 13,(13) – 0,(13).
Значить,
99х = 13,
звідки знаходимо х = 13/99.
ПРИКЛАД:
Звернути у звичайний дріб число:
2,(273).
РОЗВ'ЯЗАННЯ:
Покладемо х = 2,(273). Цей чистий періодичний дріб містить три цифри в періоді. Помноживши х на 1000, отримаємо:
1000х = 2273,(273).
Далі маємо:
1000х – х = 2273,(273) – 2,(273).
Звернути у звичайний дріб число:
0,2(54).
РОЗВ'ЯЗАННЯ:
Покладемо х = 0,2(54). Перенесемо в цьому змішаному
періодичному дробі кому вправо так, щоб вийшов чистий періодичний дріб. Для
цього достатньо х помножити на 10,
отримаємо:
10х = 2(54).
Покладемо у = 2(54) і звернемо цей чистий
періодичний дріб у звичайний. Помноживши у на 100, отримаємо:
100у = 254,(54),
100у – у = 254,(54) – 2,(54)
Звернути у звичайний дріб число:
3,254(9).
РОЗВ'ЯЗАННЯ:
Покладемо х = 3,254(9),
отримаємо 1000х =
3254,(9).
Введемо позначення
у = 1000х. Тоді маємо:
у = 3254(9), звідки 10у
= 32549,(9),
10у – у = 32549,(9) – 3254,(9),
3,254(9) = 3,255(0).
Ця обставина має місце для будь-яких десяткових дробів із
дев'яткою в періоді. Такий дріб можна подати у вигляді дробу з нулем у періоді.
Для цього достатньо лише збільшити на одиницю останній десятковий знак перед періодом.
ПРИКЛАД:
0,45(9) = 0,45(0),
14(9) = 15(0).
Нескінченний періодичний десятковий дріб дорівнює
звичайному дробу, в чисельнику якого різниця між усім числом після коми і
числом після коми до періоду, а знаменник складається з «дев'яток» і «нулів»,
причому, «дев'яток» стільки, скільки цифр у періоді, а <<нулів>>
стільки, скільки цифр після коми до періоду.
ПРИКЛАД:
Звернути у звичайний дріб число 0,41(6).
РОЗВ'ЯЗАННЯ:
Звернути у звичайний дріб число 0,10(6).
РОЗВ'ЯЗАННЯ:
Звернути у звичайний дріб число 0,(15).
РОЗВ'ЯЗАННЯ:
Звернути у звичайний дріб число 0,5(3).
РОЗВ'ЯЗАННЯ:
Число 0,666… представимо у вигляді
0,(6) = 6/9 = 2/3.
- Урок 1. Цілі числа
- Урок 2. Абсолютна величина числа
- Урок 3. Додавання цілих чисел
- Урок 4. Віднімання цілих чисел
- Урок 5. Множення цілих чисел
- Урок 6. Ділення цілих чисел
- Урок 7. Обчислення величини виразів, які стоять під знаком абсолютної величини
- Урок 8. Степінь цілого додатного числа з натуральним показником
- Урок 9. Степінь цілого відмінного числа з натуральним показником
- Урок 10. Степінь цілого додатного числа з цілим показником
- Урок 11. Степінь цілого відмінного числа з цілим показником
- Урок 12. Ділення степенів цілих чисел з натуральним показником
- Урок 13. Ділення степенів цілих чисел з цілим показником
- Урок 14. Стандартний вигляд числа
- Урок 15. Раціональні числа
- Урок 16. Додавання раціональних чисел
- Урок 17. Віднімання раціональних чисел
- Урок 18. Множення раціональних чисел
- Урок 19. Ділення раціональних чисел
- Урок 21.Степінь раціонального додатного числа з натуральним показником
- Урок 22. Степінь раціонального відмінного числа з натуральним показником
- Урок 23. Степінь раціонального додатного числа з цілим показником
- Урок 24. Степінь раціонального відмінного числа з цілим показником
- Урок 25. Ділення степенів раціональних чисел з цілим показником

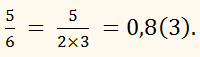














Комментариев нет:
Отправить комментарий