Основні співвідношення.
|– a| = |a|
|a – b| = |b – a|
Абсолютна величина алгебраїчної суми
двох або кількох чисел не більше від суми абсолютних величин цих чисел:
|a + b| ≤ |a| + |b|.
Знак < має місце, коли а і b числа протилежних знаків, а також, коли а і b одночасно не дорівнюють нулю. Коли а
= b
≠ 0 або коли
а
= 0, b = 0, то має місце
знак рівності.
Абсолютна величина різниці двох чисел а і b не більша від суми їх абсолютних
величин, тобто:
|a – b| ≤ |a| + |b|.
Абсолютна величина різниці двох чисел а і b не менша від різниці їх абсолютних величин, або:
|a – b| ≥ |a| – |b|.
Абсолютна величина різниці
абсолютних величин двох чисел а і
b не більша від абсолютної величини
різниці цих чисел, тобто:
||a| – |b|| ≤ |a – b|.
Спочатку слід обчислити
значення правої і лівої частини нерівності при певних значеннях а і b.
Розглянути випадок, коли числа одного знака, а потім з протилежними знаками.
ПРИКЛАД:
а = –8, b = –12;
||–8| –
|–12|| = |8 –
12| = 4.
|–8 –
(–12)| =
4.
4 = 4.
ПРИКЛАД:
а
= 6, b
= –9;
||6|
–
|–9||
< |6 –
(–9)|.
3 < 15.
Абсолютна величина добутку двох
співмножників дорівнює добуткові абсолютних величин їх.
|a1 × a2| = | a1| × | a2|.
Абсолютна величина дробу дорівнює
абсолютній величині чисельника, поділеній на абсолютну величину знаменника,
якщо знаменник не дорівнює нулю.
Завдання до уроку 7
Інші уроки:
- Урок 1. Цілі числа
- Урок 2. Абсолютна величина числа
- Урок 3. Додавання цілих чисел
- Урок 4. Віднімання цілих чисел
- Урок 5. Множення цілих чисел
- Урок 6. Ділення цілих чисел
- Урок 8. Степінь цілого додатного числа з натуральним показником
- Урок 9. Степінь цілого відмінного числа з натуральним показником
- Урок 10. Степінь цілого додатного числа з цілим показником
- Урок 11. Степінь цілого відмінного числа з цілим показником
- Урок 12. Ділення степенів цілих чисел з натуральним показником
- Урок 13. Ділення степенів цілих чисел з цілим показником
- Урок 14. Стандартний вигляд числа
- Урок 15. Раціональні числа
- Урок 16. Додавання раціональних чисел
- Урок 17. Віднімання раціональних чисел
- Урок 18. Множення раціональних чисел
- Урок 19. Ділення раціональних чисел
- Урок 20. Нескінченні періодичні десяткові дроби
- Урок 21.Степінь раціонального додатного числа з натуральним показником
- Урок 22. Степінь раціонального відмінного числа з натуральним показником
- Урок 23. Степінь раціонального додатного числа з цілим показником
- Урок 24. Степінь раціонального відмінного числа з цілим показником
- Урок 25. Ділення степенів раціональних чисел з цілим показником
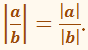
Комментариев нет:
Отправить комментарий