Графік функції у = х2.
Графіком функції
у
= х2.
є крива лінія, що
називається параболою.
Область її визначення –
множина всіх дійсних чисел.
Складемо таблицю
значень функції для деяких значень аргументу
х:
Якби на координатній площині позначили більше точок з
координатами х і у, що задовольняють формулу у = х2, вони розмістились так, як показано на малюнку.
Коли б для кожного дійсного значення х за формулою у = х2 обчислили відповідне значення у і позначили точки з такими координатами на координатній площині, дістали б
Точка з координатами (0; 0) ділить параболу на дві рівні частини, кожну з яких називають гілкою параболи, а саму точку – вершиною параболи.
Парабола проходить
через початок координат, симетрична відносно осі ординат, її вітки направлені вгору.
Побудований графік дає змогу наочно виявити
властивості функції.
– якщо х = 0, то і у = 0 (графік проходить через точку 0(0; 0));
– при всіх
значеннях х значення функції невід’ємні (нижче від осі х
немає жодної точки графіка);
– протилежним
значенням аргументу відповідають рівні значення функції (графік симетричний
відносно осі у);
– коли х < 0, функція спадає (її графік <<іде вниз>>), а коли х ˃ 0, функція зростає (її графік
напрямлений вгору).
Квадратична функція вигляду
у
= aх2
також парна, необмежена, неперіодична. Її графік також
парабола, яка проходить через початок координат і симетрична відносно осі
ординат. Але при додатних а вітки її напрямлені вгору, а при а
< 0 – вниз. Чим менша абсолютна величина а,
тем далі відходять вітки параболи від осі ординат, тим вона <<ширша>>..
Розглянемо перетворення графіку функції у = f(х). Ця побудова графіка функції
у = f(х) + n.
Графік функції у = f(х) + n виходить з графіку функції у = f(х) за допомогою паралельного перенесення уздовж осі ординат на n одиниць. Вгору при n > 0 і вниз при n < 0.
ПРИКЛАД:
Побудуємо графік функції
у = –х2 – 2.
РОЗВ’ЯЗАННЯ:
Графік функції
у = –х2 – 2.
Виходить з графіку функції
у = –х2
паралельним перенесенням уздовж осі ординат на 2 одиниці вниз, т. к. n = –2 < 0.
ПРИКЛАД:
Побудуємо графік функції
у = 2х2 + 4.
РОЗВ’ЯЗАННЯ:
Це означає, що парабола, яка є графіком функції
у = 2х2,
переміщається на чотири одиниці вгору по осі у. При цьому усі значення у збільшуються на 4.
Таблиця значень
у = 2х2.
Таблиця значень
у = 2х2 + 4.
Ми бачимо по таблиці, що вершина параболи другої функції на 4 одиниці вища за вершину параболи першої (її координати (0; 4)). А значення у другої функції на 4 більше значень у першої функції.
Квадратична функція вигляду
у
= aх2
також парна, необмежена, неперіодична. Її графік також
парабола, яка проходить через початок координат і симетрична відносно осі
ординат. Але при додатних а вітки її напрямлені вгору, а при а
< 0 – вниз. Чим менша абсолютна величина а,
тем далі відходять вітки параболи від осі ординат, тим вона <<ширша>>.
Графіком функції
у
= aх2 + b
є параболою, яку можна отримати з графіку функції
у
= aх2
с допомогою
паралельного перенесення уздовж осі у на b одиниць вгору, якщо b
> 0, або на –b одиниць вниз, якщо b
< 0.
ПРИКЛАД:
ОДЗ: (–∞;
0) ∪ (0; + ∞).
1) якщо х ˃ 0, то
2) якщо х < 0, тоОтже,Шуканий графік на рисунку.ПРИКЛАД:ОДЗ:
(–∞; 0) ∪ (0; + ∞).
Враховуючи означення модуля, матимемо: 1) якщо х ˃ 0, то |х| = х, а тому Тоді: 2) якщо х < 0, то |х| = –х, а томуОтже,Точка перетину з віссю Ох:у
= 0,
–х2 + 2 = 0, х = –√͞͞͞͞͞2.
Побудуйте графік функції:РОЗВ'ЯЗАННЯ:
ОДЗ: (–∞;
0) ∪ (0; + ∞).
Побудуйте графік функції:Користуючись
побудованим графіком, знайдіть проміжки зростання і спадання функції.
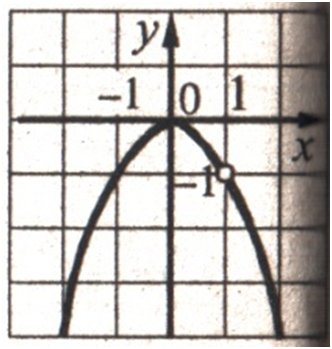
Шуканий графік на рисунку.ВІДПОВІДЬ: проміжок зростання: [0; 1],
(–1; 1).ПРИКЛАД:
РОЗВ'ЯЗАННЯ:
При х ≤ 1
графіком функції буде
частина параболи
у = х2
з
проміжком спадання (–∞; 0] і
проміжком зростання [0; 1].
Шуканий графік на рисунку.ВІДПОВІДЬ: проміжок зростання: [0; 1],
проміжки
спадання (–∞; 0] і (1; +∞):
ПРИКЛАД:
(–1; 1).ПРИКЛАД:
Побудуйте графік функції:
Областю
визначення функціїє всі
дійсні числа, крім чисел –2 і 2. ТодіГрафіком
даної функції є парабола
РОЗВ'ЯЗАННЯ:
у = х2 + 4
Побудуйте графік функції:РОЗВ'ЯЗАННЯ:Дане
рівняння рівносильне системіТому
графіком даного рівняння є парабола у = – х2 без
точки (1; –1):ПРИКЛАД:
Областю визначення функціїє всі
дійсні числа, крім чисел –2 і 2. ТодіГрафіком
даної функції є парабола
у = х2 + 1
Інші уроки:
- Урок 1. Координатна площина
- Урок 2. Діаграми
- Урок 3. Графіки
- Урок 4. Множини
- Урок 5. Що таке функція ?
- Урок 6. Аналітичній спосіб задання функції
- Урок 7. Табличний спосіб задання функції
- Урок 8. Графічний спосіб задання функції
- Урок 9. Знаходження області визначення і області значення функції аналітичним способом
- Урок 10. Знаходження області визначення і області змині за допомогою графіка
- Урок 11. Нулі функції
- Урок 12. Зростання і спадання функції
- Урок 13. Екстремальні значення функцій
- Урок 14. Симетричні функції
- Урок 15. Парні і непарні функції
- Урок 16. Функція, зворотна даною
- Урок 17. Лінійна функція
- Урок 18. Графік лінійної функції
- Урок 19. Пряма пропорційність
- Урок 20. Графік прямої пропорціональності
- Урок 21. Взаємне розташування графіків лінійних функцій
- Урок 22. Функція обернено пропорціональної залежності
- Урок 23. Графік функції обернено пропорціональної залежності
- Урок 24. Квадратична функція
- Урок 26. Графік функції у = a(х - m)2 + n
- Урок 27. Графік функції у = aх2 + bx + c
- Урок 28. Функція у = √͞͞͞͞͞х і її графік
- Урок 29. Функція у = хn і її графік
- Урок 30. Побудова графіків функцій методом геометричних перетворень




















































Комментариев нет:
Отправить комментарий