З графіка
видно, що мінімальне значення змінна у приймає при х = 0. Максимальне значення не визначається, при цьому
видно, що при зростанні х значення у також зростає.
Тоді область значень буде такою:
Е(у) = [0; +∞).
Нижче наведено декілька прикладів графіків функцій.
Графіки функцій показані жирними синіми лініями,
тонкі червоні лінії – це асимптоти, жовтими точками та лініями на осі 0у
зображено область значень відповідної функції.
Темні точки позначають, що число входить у область
значень.
Світлі точки позначають, що число не входить у
область значень.
ПРИКЛАД:
З
графіка видно, що функцією є пряма, яка паралельна осі х
і перетинає вісь у точці 2,6.
Пряма прагне в нескінченність і вправо і вліво вздовж паралельно осі х,
не перетинаючи її, а також перетинає вісь у
в точці у = 2,6 (на
графіку темна точка), отже область
визначення буде
D(у) = (–∞;
+∞).
Область значення очевидна:
Е(у) = {2,6}.
ПРИКЛАД:

З
графіку видно, що функція прагне в нескінченність і управо і вліво уздовж осі х,
не перетинаючи її (на
графіці біла точка), а також
перетинає вісь у в точці
у
= 9 (на графіці темна точка),
означає область визначення буде
D(у) = (–∞;
+∞).
Область значення очевидна:
Е(у) = (0; 9].
Нуль не входить в область значень, а
дев'ять входить.
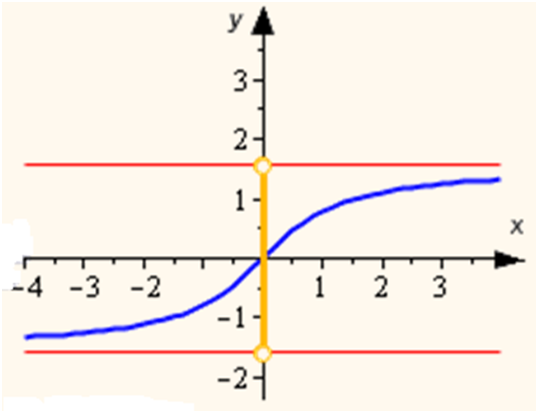
ПРИКЛАД:
З
графіка видно, що функцією є крива, яка перетинає вісь у точці 0.
Крива прагне в нескінченність і вправо і вліво, максимум якої +1,
а мінімум –1 (на графіку темні точки), отже
область визначення буде
D(у) = (–∞;
+∞).
Область значення очевидна:
Е(у) = [+1; –1].
ПРИКЛАД:
Знайдіть
область визначення та область значення функції
у = arctg x
З
графіка видно, що функцією є крива, яка перетинає вісь у точці 0. Крива прагне
в нескінченність і вправо і вліво. Прагне до точок + π/2 і – π/2 (на графіку світлі точки),
отже область визначення буде
D(у) = (–∞;
+∞).
Область значення очевидна:
Е(у) = (–π/2; + π/2).
ПРИКЛАД:
Знайдіть
область визначення та область значення функції
у = е–х
– 2
З
графіка видно, що функцією є крива, яка перетинає вісь у точці –1.
Крива прагне нескінченності і вправо і вліво. Прагне до точки –2
(на графіку світла точка), отже область визначення буде
D(у) = (–∞;
+∞).
Область значення очевидна:
Е(у) = (–2; +∞).
ПРИКЛАД:
Знайдіть область визначення та область значення функції
за графіком.РОЗВ'ЯЗАННЯ:З
графіка видно, що функцією є дві криві, одна з яких перетинає вісь у в точці 0.
Криві прагне в нескінченність і вправо і вліво, а також прагнуть асимптота х = 2,
значить область визначення буде
D(у) = (–∞;
2) ∪ (2; +∞).
Область значення очевидна:
Е(у) = (–∞; 0] ∪ [4; +∞).
ПРИКЛАД:
З
графіка видно, що функцією є дві криві, одна з яких перетинає вісь у
в точці 0.
Криві прагне в нескінченність і вправо і вліво, а також прагнуть до асимптот х = 2 і у = 1, отже область визначення буде
D(у) = (–∞;
2) ∪ (2; +∞).
Область значення очевидна:
Е(у) = (–∞; 1) ∪ (1; +∞).
ПРИКЛАД:
Область значення очевидна:
Е(у) = [–6; –2] ∪ {–1} ∪ (0; +∞).
ПРИКЛАД:
Область значення очевидна:
- Урок 1. Координатна площина
- Урок 2. Діаграми
- Урок 3. Графіки
- Урок 4. Множини
- Урок 5. Що таке функція ?
- Урок 6. Аналітичній спосіб задання функції
- Урок 7. Табличний спосіб задання функції
- Урок 8. Графічний спосіб задання функції
- Урок 9. Знаходження області визначення і області значення функції аналітичним способом
- Урок 11. Нулі функції
- Урок 12. Зростання і спадання функції
- Урок 13. Екстремальні значення функцій
- Урок 14. Симетричні функції
- Урок 15. Парні і непарні функції
- Урок 16. Функція, зворотна даною
- Урок 17. Лінійна функція
- Урок 18. Графік лінійної функції
- Урок 19. Пряма пропорційність
- Урок 20. Графік прямої пропорціональності
- Урок 21. Взаємне розташування графіків лінійних функцій
- Урок 22. Функція обернено пропорціональної залежності
- Урок 23. Графік функції обернено пропорціональної залежності
- Урок 24. Квадратична функція
- Урок 25. Графік функції у = aх2 + b
- Урок 26. Графік функції у = a(х - m)2 + n
- Урок 27. Графік функції у = aх2 + bx + c
- Урок 28. Функція у = √͞͞͞͞͞х і її графік
- Урок 29. Функція у = хn і її графік
- Урок 30. Побудова графіків функцій методом геометричних перетворень














Комментариев нет:
Отправить комментарий